题目内容
点P是x轴正半轴的一个动点,过点P作x轴的垂线PA交双曲线y=| 1 |
| x |
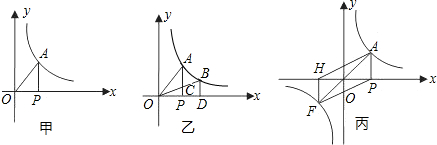
(1)如图甲,当点P在x轴的正方向上运动时,Rt△AOP的面积大小是否变化?若不变,请求出Rt△AOP的面积;若改变,试说明理由;
(2)如图乙,在x轴上的点P的右侧有一点D,过点D作x轴的垂线交双曲线于点B,连接BO交AP于点C,设△AOP的面积是S1,梯形BCPD的面积为S2,则S1与S2的大小关系是S1S2(选填“>”、“<”、“=”);
(3)如图丙,AO的延长线与双曲线y=
| 1 |
| x |
分析:(1)本题还可依据比例系数k的几何意义,得出两个三角形的面积都等于
|k|=
,因而当点P在x轴的正方向上运动时,Rt△AOP的面积大小不变;
(2)根据(1)可以得到△BDO的面积,因而S1>S2.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据(1)可以得到△BDO的面积,因而S1>S2.
解答:解:(1)Rt△AOP的面积不变,S△AOP=xy=x×
×
=
;
(2)根据△AOP的面积等于S1,△BOD的面积大于S2,S1>S2;
(3)设A的坐标是(a,b),根据反比例函数是中心对称图形,因而F点的坐标是(-a,-b),则AP=b,HP=2a,则四边形APFH的面积是2ab,据(a,b)在双曲线y=
的图象上,因而ab=1,则四边形APFH的面积是2ab=2.
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据△AOP的面积等于S1,△BOD的面积大于S2,S1>S2;
(3)设A的坐标是(a,b),根据反比例函数是中心对称图形,因而F点的坐标是(-a,-b),则AP=b,HP=2a,则四边形APFH的面积是2ab,据(a,b)在双曲线y=
| 1 |
| x |
点评:本题考查函数图象交点坐标的求法及反比例函数的比例系数k与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=
|k|.
| 1 |
| 2 |

练习册系列答案
相关题目
 如图,将一矩形OABC放在直角坐标系中,O为坐标原点.点A在y轴正半轴上.点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数
如图,将一矩形OABC放在直角坐标系中,O为坐标原点.点A在y轴正半轴上.点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数
 (2012•梓潼县一模)如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线
(2012•梓潼县一模)如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线 (2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
(2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.