题目内容
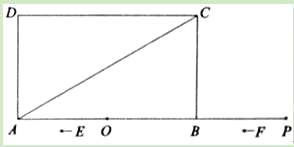
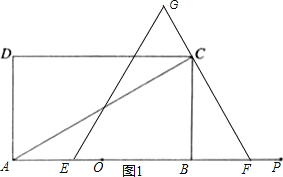
【题目】如图,矩形ABCD中,AB=6,BC=2![]() ,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t,使△AOH是等腰三角形?若存大,求出对应的t的值;若不存在,请说明理由.
【答案】(1)t=1;(2)详见解析;(3)当t=3﹣![]() ,t=3+
,t=3+![]() ,t=2,t=4,t=0时,△AOH是等腰三角形.
,t=2,t=4,t=0时,△AOH是等腰三角形.
【解析】
(1)当边FG恰好经过点C时,由∠CFB=60°得BF=3﹣t,在Rt△CBF中,根据三角函数求得t的值;
(2)根据运动的时间为t不同的取值范围,求等边△EFG和矩形ABCD重叠部分的面积为S的值,当0≤t<1时,重叠部分是直角梯形,面积S等于梯形的面积,
当1≤t<3时,重叠部分是S梯形MKFE﹣S△QBF,当3≤t<4时,重叠部分是S梯形MKFE,当4≤t<6时,重叠部分是正三角形的面积;
(3)当AH=AO=3时,AM=![]() AH=
AH=![]() ,在Rt△AME中,由cos∠MAE=
,在Rt△AME中,由cos∠MAE=![]() 即cos30°=
即cos30°=![]() ,得AE=
,得AE=![]() ,即3﹣t=
,即3﹣t=![]() 或t﹣3=
或t﹣3=![]() ,求出t=3﹣
,求出t=3﹣![]() 或t=3+
或t=3+![]() ;
;
当AH=HO时,∠HOA=∠HAO=30°,又因为∠HEO=60°得到∠EHO=90°EO=2HE=2AE,再由AE+2AE=3,求出AE=1,即3﹣t=1或t﹣3=1,求出t=2或t=4;
当OH=OA=时∠HOB=∠OAH=30°,所以∠HOB=60°=∠HEB,得到点E和点O重合,从而求出t的值
如图1(1),当边FG恰好经过点C时,
∵∠CFB=60°,
∴BF=3﹣t,
在Rt△CBF中,
∵BC=2![]() ,tan∠CFB=
,tan∠CFB=![]() ,
,
∴tan60=![]() ,
,
解得BF=2,即3﹣t=2,
∴t=1,
当边FG恰好经过点C时,t=1;
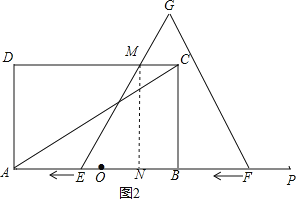
(2)如图2,过点M作MN⊥AB于N,
当0≤t<1时,
∵tan60°=![]() ,
,
∴EN=2,
∵EB=3+t,NB=3+t﹣2=1+t,
∴MC=1+t,
∴S=![]() (MC+EB)BC=2
(MC+EB)BC=2![]() t+4
t+4![]() ;
;
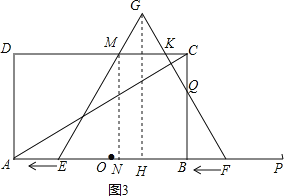
如图3,当1≤t<3时,
∵MN=2![]() EF=OP=6,
EF=OP=6,
GH=6×![]() =3
=3![]() ,
,
∴![]() ,
,
∴MK=2,
∵EB=3+t,BF=3﹣t,BQ=![]() t﹣
t﹣![]() ,
,
∴S=S梯形MKFE﹣S△QBF=﹣![]() t2+3
t2+3![]() t+
t+![]() ;
;
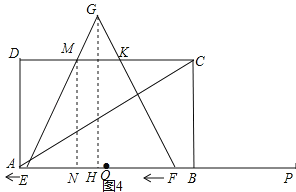
如图4,当3≤t<4时,
∵MN=2![]() ,EF=6﹣2(t﹣3)=12﹣2t,
,EF=6﹣2(t﹣3)=12﹣2t,
∴GH=(12﹣2t)×![]() =6
=6![]() ﹣
﹣![]() t,∴
t,∴![]() ,
,
∴MK=8﹣2t,
∴S=﹣4![]() t+20
t+20![]() ;
;
当4≤t<6时,
∵EF=12﹣2t,
∴高为:EFsin60°=![]() EF,
EF,
∴S=![]() t2﹣12
t2﹣12![]() t+36
t+36![]() ;
;
(3)存在.
在Rt△ABC中,tan![]() ,∴∠CAB=30°
,∴∠CAB=30°
∵∠HEO=60°,
∴∠HAE=∠AHE 30°,
∴AE=HE=3﹣t或t﹣3,
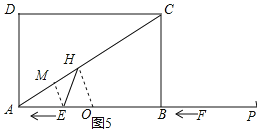
如图5,当AH=AO=3时,
过点E作EM⊥AH与M,
则AM=![]() AH=
AH=![]() ,
,
在Rt△AME中,
cos∠MAE=![]() 即cos30°=
即cos30°=![]() ,
,
∴AE![]() ,
,
即3﹣t=![]() 或t﹣3=
或t﹣3=![]() ;
;
∴t=3﹣![]() 或t=3+
或t=3+![]() ;
;
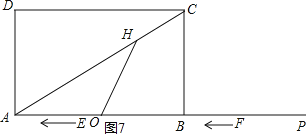
如图6,当AH=HO时,∠HOA=∠HAO=30°,
∵∠HEO=60°,
∴∠EHO=90°,EO=2HE=2AE,
∵AE+2AE=3,
∴AE=1,即3﹣t=1或t﹣3=1,
∴t=2或t=4;
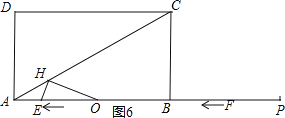
如图7,当OH=OA=时,
∠HOB=∠OAH=30°,
∴∠HOB=60°=∠HEB,
∴点E和点O重合,
∴AE=AO=3,
当E刚开始时,3﹣t=3,
当E返回时t﹣3=3,
∴t=0,t=6(舍去),
综上所述当t=3﹣![]() ,t=3+
,t=3+![]() ,t=2,t=4,t=0时,△AOH是等腰三角形.
,t=2,t=4,t=0时,△AOH是等腰三角形.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】某商店新进一种台灯.这种台灯的成本价为每个30元,经调查发现,这种台灯每天的销售量y(单位:个)是销售单价x(单位:元)(30≤x≤60)的一次函数.
x | 30 | 35 | 40 | 45 | 50 |
y | 30 | 25 | 20 | 15 | 10 |
(1)求销售量y与销售单价x之间的函数表达式;
(2)设这种台灯每天的销售利润为w元.这种台灯销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?