题目内容
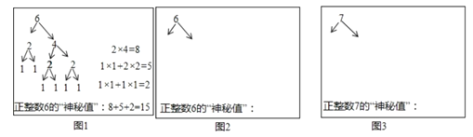
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3).
(1)求抛物线y=x2+bx+c的表达式;
(2)点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;
(3)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.
【答案】(1)y=x2﹣4x+3;(2)(2,﹣1);(3)![]() .
.
【解析】试题分析:(1)利用待定系数法求抛物线解析式;
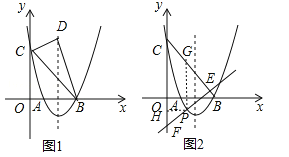
(2)如图1,设D(2,y),利用两点间的距离公式得到BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,然后讨论:当BD为斜边时得到18+4+(y﹣3)2=1+y2;当CD为斜边时得到4+(y﹣3)2=1+y2+18,再分别解方程即可得到对应D的坐标;
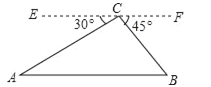
(3)先证明∠CEF=90°得到△ECF为等腰直角三角形,作PH⊥y轴于H,PG∥y轴交BC于G,如图2,△EPG、△PHF都为等腰直角三角形,则PE=![]() PG,PF=
PG,PF=![]() PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),接着利用t表示PF、PE,这样PE+EF=2PE+PF=﹣
PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),接着利用t表示PF、PE,这样PE+EF=2PE+PF=﹣![]() t2+4
t2+4![]() t,然后利用二次函数的性质解决问题.
t,然后利用二次函数的性质解决问题.
试题解析:解:(1)把B(3,0),C(0,3)代入y=x2+bx+c得: ![]() ,解得:
,解得: ![]() ,∴抛物线y=x2+bx+c的表达式为y=x2﹣4x+3;
,∴抛物线y=x2+bx+c的表达式为y=x2﹣4x+3;
(2)如图1,抛物线的对称轴为直线x=﹣![]() =2,设D(2,y),B(3,0),C(0,3),∴BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,当△BCD是以BC为直角边,BD为斜边的直角三角形时,BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,解得:y=5,此时D点坐标为(2,5);
=2,设D(2,y),B(3,0),C(0,3),∴BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,当△BCD是以BC为直角边,BD为斜边的直角三角形时,BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,解得:y=5,此时D点坐标为(2,5);
当△BCD是以BC为直角边,CD为斜边的直角三角形时,BC2+DB2=DC2,即4+(y﹣3)2=1+y2+18,解得:y=﹣1,此时D点坐标为(2,﹣1);
(3)易得BC的解析式为y=﹣x+3.∵直线y=x+m与直线y=x平行,∴直线y=﹣x+3与直线y=x+m垂直,∴∠CEF=90°,∴△ECF为等腰直角三角形,作PH⊥y轴于H,PG∥y轴交BC于G,如图2,△EPG、△PHF都为等腰直角三角形,PE=![]() PG,PF=
PG,PF=![]() PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),∴PF=
PH,设P(t,t2﹣4t+3)(1<t<3),则G(t,﹣t+3),∴PF=![]() PH=
PH=![]() t,PG=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,∴PE=
t,PG=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,∴PE=![]() PG=﹣
PG=﹣![]() t2+
t2+![]() t,∴PE+EF=PE+PE+PF=2PE+PF=﹣
t,∴PE+EF=PE+PE+PF=2PE+PF=﹣![]() t2+3
t2+3![]() t+
t+![]() t=﹣
t=﹣![]() t2+4
t2+4![]() t=﹣
t=﹣![]() (t﹣2)2+4
(t﹣2)2+4![]() ,当t=2时,PE+EF的最大值为4
,当t=2时,PE+EF的最大值为4![]() .
.

【题目】甲、乙两名同学进入八年级后,某科6次考试成绩如图所示:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 75 | 75 | ||
乙 | 33.3 | 70 |
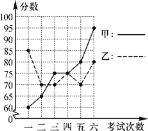
(1)请根据统计图填写上表:
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行
①从平均数和方差相结合看,你得出什么结论;
②从折线图上两名同学分数的走势上看,你认为反映出什么问题?