Question

【题目】已知正六边形的边长为，点为六边形内任一点，则点到各边距离之和为______．

Answer 1

【答案】18

【解析】

过P作AB的垂线，交AB、DE分别为H、K，连接BD，由正六边形的性质可知AB∥DE，AF∥CD，BC∥EF，故HK⊥DE，过C作CG⊥BD，由等腰三角形的性质及正六边形的内角和定理可知，DB⊥AB⊥DE，再由锐角三角函数的定义可求出BG的长，进而可求出BD的长，由正六边形的性质可知点P到AF与CD的距离和及P到EF、BC的距离和均为BD的长，故可得出结论．

解：过P作AB的垂线，交AB、DE分别为H、K，连接BD，

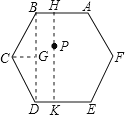
∵六边形ABCDEF是正六边形，

∴AB∥DE，AF∥CD，BC∥EF，且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长，

∵BC＝CD，∠BCD＝∠ABC＝∠CDE＝120°，

∴∠CBD＝∠BDC＝30°，

∴BD∥HK，且BD＝HK，

∵CG⊥BD，

∴BD＝2BG＝2×BC×cos∠CBD＝2×2＝6，

∴点P到各边距离之和为3BD＝3×6＝18．

故答案为：18．