题目内容
【题目】如图，点
是直角三角形
斜边
上一动点（不与点
，
重合），作直线
，分别过点，向直线作垂线，垂足分别为
，
，
为斜边的中点.
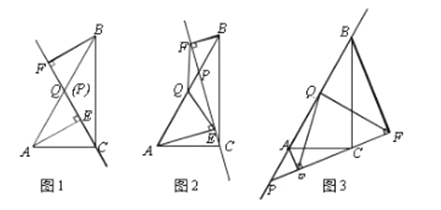
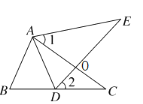
（1）如图1，当点与点重合时，
与
的位置关系是______，
与
的数量关系是______；
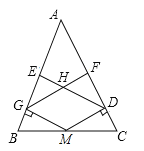
（2）如图2，当点在线段上（不与点重合）时，试猜想与的数量关系，并说明理由；
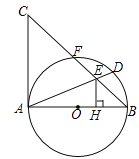
（3）如图3，当点在线段
的延长线上时，此时（2）中的结论是否仍成立？请说明理由.
【答案】（1）AE∥BF，QE=QF，（2）QE=QF，证明见解析；（3）当点P在线段BA（或AB）的延长线上时，此时（2）中的结论成立，证明见解析.
【解析】
（1）根据AAS推出△AEQ≌△BFQ即可得出答案；
（2）延长EQ交BF于D，求出△AEQ≌△BDQ，根据全等三角形的性质得出EQ=QD，根据直角三角形斜边上中点性质得出即可；
（3）延长EQ交FB于D，求出△AEQ≌△BDQ，根据全等三角形的性质得出EQ=QD，根据直角三角形斜边上中点性质得出即可
（1）如图1，
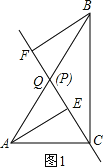
当点P与点Q重合时，AE与BF的位置关系是AE∥BF，QE与QF的数量关系是AE=BF，
理由：
∵Q为AB的中点，
∴AQ=BQ，
∵AE⊥CQ，BF⊥CQ，
∴AE∥BF，∠AEQ=∠BFQ=90°，
在△AEQ和△BFQ中
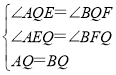
∴△AEQ≌△BFQ（AAS），
∴QE=QF，
（2）
QE=QF，
证明：如图2，延长EQ交BF于D，
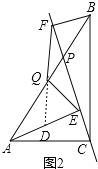
∵由（1）知：AE∥BF，
∴∠AEQ=∠BDQ，
在△AEQ和△BDQ中
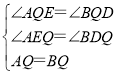
∴△AEQ≌△BDQ（AAS），
∴EQ=DQ，
∵∠BFE=90°，
∴QE=QF；
（3）当点P在线段BA（或AB）的延长线上时，此时（2）中的结论成立，
证明：延长EQ交FB于D，如图3，
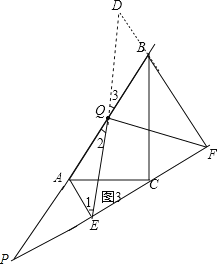
∵由（1）知：AE∥BF，
∴∠AEQ=∠BDQ，
在△AEQ和△BDQ中
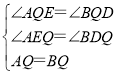
∴△AEQ≌△BDQ（AAS），
∴EQ=DQ，
∵∠BFE=90°，
∴QE=QF．
