题目内容
【题目】问题情境:
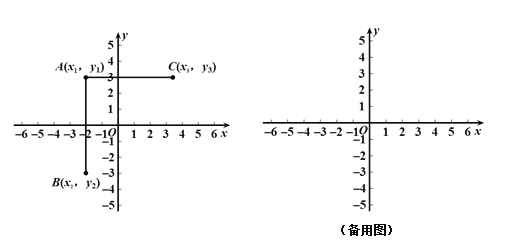
如图,在平面直角坐标系中有三点A(x1,y1),B(x2,y2),C(x3,y3),小明在学习中发现,当x1=x2,AB∥y轴,线段AB的长度为|y1﹣y2|;当y1=y3,AC∥x轴,线段AC的长度为|x1﹣x3|.
初步应用
(1)若点A(﹣1,1)、B(2,1),则AB∥ 轴(填“x”或“y”);
(2)若点C(1,﹣2),CD∥y轴,且点D在x轴上,则CD= ;
(3)若点E(﹣3,2),点F(t,﹣4),且EF∥y轴,t= ;
拓展探索:
已知P(3,﹣3),PQ∥y轴.
(1)若三角形OPQ的面积为3,求满足条件的点Q的坐标.
(2)若PQ=a,将点Q向右平移b个单位长度到达点M,已知点M在第一象限角平分线上,请直接写出a,b之间满足的关系.
【答案】初步应用:(1)x;(2)2;(3)-3;拓展探索:(1)Q点坐标为(3,-1)或(3,-5);(2)a﹣b=6.
【解析】
初步应用:(1)根据若![]() ,即可得出结论;
,即可得出结论;
(2)由C(1,﹣2),CD∥y轴,且点D在x轴上,可得D的坐标,再根据![]() 进行计算即可,
进行计算即可,
(3)由EF∥y轴,可得![]() ,从而可得答案,
,从而可得答案,
拓展探索:
(1)利用P(3,﹣3),PQ∥y轴,三角形OPQ的面积为3,可得![]() 的长度,结合
的长度,结合![]() 的位置直接得到答案,
的位置直接得到答案,
(2)利用P(3,﹣3),PQ∥y轴,PQ=a,写出![]() 的坐标,再根据平移规律得到
的坐标,再根据平移规律得到![]() 的坐标,利用
的坐标,利用![]() 的位置列方程得数量关系.
的位置列方程得数量关系.
解:(1)![]() A(﹣1,1)、B(2,1),
A(﹣1,1)、B(2,1),
![]() ,
,
![]() 轴,
轴,
故答案为:![]() .
.
(2)![]() C(1,﹣2),CD∥y轴,且点D在x轴上,
C(1,﹣2),CD∥y轴,且点D在x轴上,
![]() ,
,
![]()
故答案为:2.
(3)![]() EF∥y轴,
EF∥y轴,
![]()
![]() ,
,
![]() E(﹣3,2),点F(t,﹣4),
E(﹣3,2),点F(t,﹣4),
![]()
![]()
故答案为:![]()
拓展探索:
(1)如图:![]() P(3,﹣3),PQ∥y轴,
P(3,﹣3),PQ∥y轴,
![]()
![]()
![]() ,
,
同理:![]()
![]() .
.
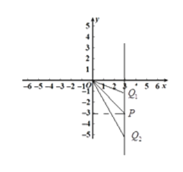
故答案为:(3,-1)或(3,-5)
(2)![]() PQ=a,P(3,﹣3),PQ∥y轴,
PQ=a,P(3,﹣3),PQ∥y轴,
![]() 或
或![]() (不合题意舍去)
(不合题意舍去)
![]() 往右平移
往右平移![]() 个单位长度后到点M,则
个单位长度后到点M,则![]() 坐标为
坐标为![]() ,
,
![]()
![]() 在第一象限的角平分线上,
在第一象限的角平分线上,
![]()
![]()
故答案为:![]()

 综合自测系列答案
综合自测系列答案【题目】已知三角形A1B1C1是由三角形ABC经过平移得到的,其中A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如表所示:
三角形ABC | A(0,0) | B(﹣1,2) | C(2,5) |
三角形A1B1C1 | A1(a,2) | B1(4,b) | C1(7,7) |
(1)观察表中各对应点坐标的变化,填空a= ,b= ;
(2)在图中的平面直角坐标系中画出三角形ABC及三角形A1B1C1;
(3)P(m,n)为三角形ABC中任意一点,则平移后对应点P'的坐标为 .