Question

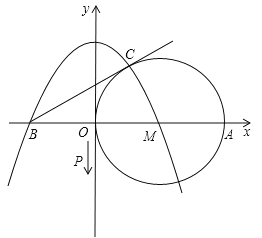
【题目】如图，在平面直角坐标系中，以点M（2，0）为圆心的⊙M与y轴相切于原点O，过点B（﹣2，0）作⊙M的切线，切点为C，抛物线经过点B和点M．

（1）求这条抛物线解析式；

（2）求点C的坐标，并判断点C是否在（1）中抛物线上；

（3）动点P从原点O出发，沿y轴负半轴以每秒1个单位长的速度向下运动，当运动t秒时到达点Q处．此时△BOQ与△MCB全等，求t的值．

Answer 1

【答案】（1）y＝﹣x2+；（2）点C在（1）的抛物线上；（3）t＝2．

【解析】

（1）利用待定系数法即可确定该抛物线的解析式．

（2）连接圆心和切点、再过点C作x轴的垂线，利用射影定理和勾股定理即可确定点C的坐标，再代入（1）的抛物线中进行验证即可．

（3）△BCM和△BOQ中，OB＝CM，∠BOQ＝∠BCM＝90°，若两个三角形全等，必须满足OQ＝BC，求出BC长即可．

（1）将点M（2，0）、B（﹣2，0）代入 yx2+bx+c 中，得：

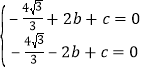
解得：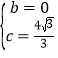

∴抛物线的解析式：yx2．

（2）连接MC，则MC⊥BC；过点C作CD⊥x轴于D，如图，在Rt△BCM中，CD⊥BM，CM＝2，BM＝4，则：

DM1，CD，OD＝OM﹣DM＝1，∴C（1，）．

当x＝1时，yx2，所以点C在（1）的抛物线上．

（3）△BCM和△BOQ中，OB＝CM＝2，∠BOQ＝∠BCM＝90°，若两三角形全等，则：

OQ＝BC，∴当t＝2时，△MCB和△BOQ全等．