��Ŀ����
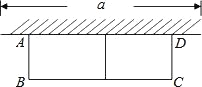
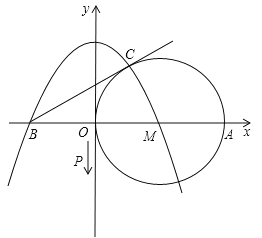
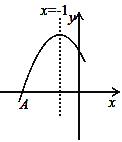
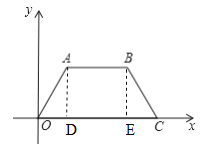
����Ŀ����ͼ����ֱ������ϵxOy����һ����ABCO������C��x�������ϣ�A��B�����ڵ�һ���ޣ���AB��CO��AO��BC��2��AB��3��OC��5����P��x���ϣ��ӵ㣨��2��0����������ÿ��1����λ���ȵ��ٶ���x�����������˶���ͬʱ������P��ֱ��l��ʹֱ��l��x����������н�Ϊ30�㣮���P�˶���t�룬ֱ��lɨ������ABCO�����ΪSɨ��
��1����A��B��������ꣻ
��2����t��2��ʱ����Sɨ��ֵ��
��3����Sɨ��t�ĺ�����ϵʽ�������ֱ��lɨ������ABCO�����![]() ʱ��P�����꣮
ʱ��P�����꣮

���𰸡���1����1��![]() ������4��
������4��![]() ������2��
������2��![]() ����3��
����3��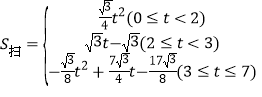 ��P��������5��2
��P��������5��2![]() ��0����
��0����
��������
��1�����IJ��һ�����A�ĺ���������A��B��x��Ĵ������ڹ�����ֱ���������и���OA�ij������IJ���������εĸ�A��������꣮�ó�A�����������ƽ��3����λ����B���������
��2����t��2ʱ��P��O�����غ��������ֱ��l��AB�Ľ���ΪD����ôAD��2����AD���ϵĸ߾���A������������ɴ˿������ADO�������ֱ��lɨ���������
��3������Ҫ�������������������
����P��ԭ�����������0��t��2ʱ���غϲ����Ǹ��������������ֱ��l��AO��AB�ֱ���E��F���ɸ��ݡ�AEF�ס�AOD�������Ʊ��������������ɵó�S��t�ĺ�����ϵʽ��
����P��O���Ҳࣨ������O�غϣ�����F����B�����ʱ������2��t��3ʱ��ɨ�������Ǹ��������ɸ������ε�������㷽�����ɵó�ֱ��lɨ�����ֵ������Ҳ���ܵó�S��t�ĺ�����ϵʽ��
����P����C����ࣨ������C���غϣ���F����B���Ҳࣨ������B���غϣ�������3��t��7ʱ��ɨ�������Ǹ����������������ABCO�������ȥ��MPC��������ó�S��t�ĺ�����ϵʽ��
��1����A��AD��OC��D����B��BE��OC��E����ADEB�Ǿ�����
��ADEB�Ǿ�������AD=BE=3��
��AO=BC�����AOD�ա�BCE����OD=CE=��OC��AB����2=1��
��AO=2����AD=![]() =
=![]() ����A��1��
����A��1��![]() ����
����
��OE=OD+DE=1+3=4��BE=AD=![]() ����B��4��
����B��4��![]() ����
����
��BC=2EC�����EBC=30�㣬���OCB=60�㣮
��2����t��2ʱ��P��O�����غ��������ֱ��l��AB�Ľ���ΪD����ôAD��2����AD���ϵĸ߾���A�������������Sɨ=![]() =
=![]() ��
��
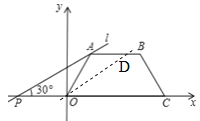
��3���������������������0��t��2ʱ����ͼ1����AEF�ס�AOD��![]() ����Sɨ
����Sɨ![]() t2��
t2��
����2��t��3ʱ����ͼ2��Sɨ��S��AOD+S��DOPF![]() ��t��2������Sɨ
��t��2������Sɨ![]() ��
��
����3��t��7ʱ����ͼ3����B��ֱ��EB��ֱ��l��OC��E��
�ߡ�BEC=30�㣬��OCB=60�㣬���CBE=90�㣬��EC=2BC=4����S��CEB=![]() ��CP=7��t��
��CP=7��t��
��MP��BE����![]() ����S��CPM��
����S��CPM��![]() ����Sɨ��4
����Sɨ��4![]() S��CPM��4
S��CPM��4![]() ����Sɨ
����Sɨ![]() t2
t2![]()
����������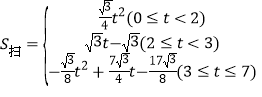 ��
��
��![]() t2
t2![]() ����t2��14t+41��0��t1��7��2
����t2��14t+41��0��t1��7��2![]() ��t2��7+2
��t2��7+2![]() 7���ᣩ����P������Ϊ��5��2
7���ᣩ����P������Ϊ��5��2![]() ��0����
��0����