题目内容
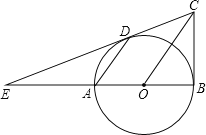
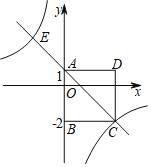
【题目】如图，四边形ABCD是正方形，点A的坐标是（0，1），点B的坐标是（0，﹣2），反比例函数y＝
的图象经过点C，一次函数y＝ax+b的图象经过A、C两点，两函数图象的另一个交点E的坐标是（m，3）．
（1）分别求出一次函数与反比例函数的解析式．
（2）求出m的值，并根据图象回答：当x为何值时，一次函数的值大于反比例函数的值．
（3）若点P是反比例函数图象上的一点，△AOP的面积恰好等于正方形ABCD的面积，求点P坐标．
【答案】（1）y＝﹣
；y＝﹣x+1；（2）x＜﹣2或0＜x＜3；（3）P点坐标为（18，﹣
）或（﹣18，）
【解析】
（1）先根据A点和B点坐标得到正方形的边长，则BC＝3，于是可得到C（3，﹣2），然后利用待定系数法求反比例函数与一次函数的解析式；
（2）将点E的坐标（m，3）代入反比例函数的解析式即可求出m的值，根据图象找出一次函数落在反比例函数图象上方的部分对应的自变量的取值范围即可；
（3）设P（t，﹣
），根据三角形面积公式和正方形面积公式得到
×1×|t|＝3×3，然后解绝对值方程求出t即可得到P点坐标．
（1）∵点A的坐标为（0，1），点B的坐标为（0，﹣2），
∴AB＝1+2＝3，
∵四边形ABCD为正方形，
∴BC＝AB＝3，
∴C（3，﹣2），
把C（3，﹣2）代入y＝
，得k＝3×（﹣2）＝﹣6，
∴反比例函数解析式为y＝﹣；
把C（3，﹣2），A（0，1）代入y＝ax+b，
得
，解得
，
∴一次函数解析式为y＝﹣x+1；
（2）∵反比例函数y＝﹣的图象过点E（m，3），
∴m＝﹣2，
∴E点的坐标为（﹣2，3）；
由图象可知，当x＜﹣2或0＜x＜3时，一次函数落在反比例函数图象上方，
即当x＜﹣2或0＜x＜3时，一次函数的值大于反比例函数的值；
（3）设P（t，﹣），
∵△AOP的面积恰好等于正方形ABCD的面积，
∴×1×|t|＝3×3，解得t＝18或t＝﹣18，
∴P点坐标为（18，﹣）或（﹣18，）．
【题目】为弘扬传统文化，某校开展了“传承经典文化，阅读经典名著”活动．为了解七、八年级学生(七、八年级各有600名学生)的阅读效果，该校举行了经典文化知识竞赛．现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析，过程如下：
收集数据：
七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77．
八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41．
整理数据：
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据：
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据：
(1)由上表填空：a= ，b= ，c= ，d= ．
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人？
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好，请说明理由．