题目内容
若x1、x2是一元二次方程ax2+bx+c=0（a≠0，a、b、c 为系数且为常数）的两个根，则x1+x2=-
、x1•x2=
，这个定理叫做韦达定理．如：x1、x2是方程x2+2x-1=0的两个根，则x1+x2=-2、x1•x2=-1．
若x1、x2是一元两次方程2x2+mx-2m+1=0的两个实数根．试求：
（1）x1+x2与x1•x2的值（用含有m的代数式表示）．
（2）若x12+x22=4，试求m的值．
| b |
| a |
| c |
| a |
若x1、x2是一元两次方程2x2+mx-2m+1=0的两个实数根．试求：
（1）x1+x2与x1•x2的值（用含有m的代数式表示）．
（2）若x12+x22=4，试求m的值．
分析：（1）由x1、x2是一元两次方程2x2+mx-2m+1=0的两个实数根，根据根与系数的关系可得x1+x2=-
、x1•x2=
；
（2）由x12+x22=（x1+x2）2-2x1•x2=4，即可得方程
+2m-1=4，解此方程即可求得答案．
| m |
| 2 |
| 1-2m |
| 2 |
（2）由x12+x22=（x1+x2）2-2x1•x2=4，即可得方程
| m2 |
| 4 |
解答：解：（1）∵x1、x2是一元两次方程2x2+mx-2m+1=0的两个实数根，
∴x1+x2=-
、x1•x2=
；
（2）∵x12+x22=（x1+x2）2-2x1•x2=（-
）2-2×
=4，
即
+2m-1=4，
解方程得：m1=2，m2=-10，
当m=2时，原方程为：2x2+2x-3=0，△=28＞0，符合题意；
当m=-10时，原方程为：2x2-10x+21=0，△=-68＜0，不符合题意，舍去．
∴m的值为2．
∴x1+x2=-
| m |
| 2 |
| 1-2m |
| 2 |
（2）∵x12+x22=（x1+x2）2-2x1•x2=（-
| m |
| 2 |
| 1-2m |
| 2 |
即
| m2 |
| 4 |
解方程得：m1=2，m2=-10，
当m=2时，原方程为：2x2+2x-3=0，△=28＞0，符合题意；
当m=-10时，原方程为：2x2-10x+21=0，△=-68＜0，不符合题意，舍去．
∴m的值为2．
点评：此题考查了一元二次方程根与系数的关系、根的判别式．此题难度较大，注意掌握若二次项系数不为1，x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-
，x1x2=
知识的应用．
| b |
| a |
| c |
| a |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
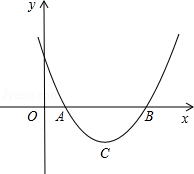
（2012•兰州）若x1、x2是关于一元二次方程ax2+bx+c（a≠0）的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1+x2=-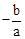
，x1•x2＝
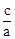．把它称为一元二次方程根与系数关系定理．如果设二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0)．利用根与系数关系定理可以得到A、B连个交点间的距离为：AB＝|x1－x2|＝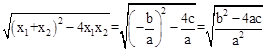
。
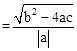