题目内容
若x1、x2是一元二次方程x2+2x-3=0的二个根，则x1•x2的值是（ ）A．2
B．-2
C．3
D．-3
【答案】分析：由x1、x2是一元二次方程x2+2x-3=0的二个根，根据根与系数的关系，即可求得x1•x2的值．
解答：解：∵x1、x2是一元二次方程x2+2x-3=0的二个根，
∴x1•x2=-3．
故选D．
点评：此题考查了根与系数的关系．此题比较简单，注意掌握根与系数的关系：若一元二次方程x2+px+q=0的两个根分别是x1、x2，则x1+x2=-p，x1•x2=q．
解答：解：∵x1、x2是一元二次方程x2+2x-3=0的二个根，
∴x1•x2=-3．
故选D．
点评：此题考查了根与系数的关系．此题比较简单，注意掌握根与系数的关系：若一元二次方程x2+px+q=0的两个根分别是x1、x2，则x1+x2=-p，x1•x2=q．
练习册系列答案
相关题目
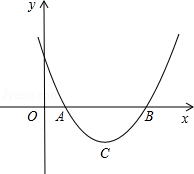
（2012•兰州）若x1、x2是关于一元二次方程ax2+bx+c（a≠0）的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1+x2=-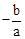
，x1•x2＝
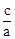．把它称为一元二次方程根与系数关系定理．如果设二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的两个交点为A(x1，0)，B(x2，0)．利用根与系数关系定理可以得到A、B连个交点间的距离为：AB＝|x1－x2|＝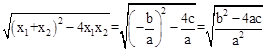
。
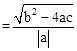