题目内容
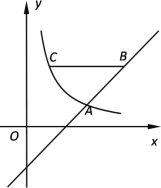
【题目】如图,在直角坐标系![]() 中,反比例函数图像与直线
中,反比例函数图像与直线![]() 相交于横坐标为3的点A.
相交于横坐标为3的点A.
(1)求反比例函数的解析式;
(2)如果点B在直线![]() 上,点C在反比例函数图像上,BC//
上,点C在反比例函数图像上,BC//![]() 轴,BC= 4,且BC在点A上方,求点B的坐标.
轴,BC= 4,且BC在点A上方,求点B的坐标.
【答案】(1)![]() ; (2)点B的坐标为(5,3).
; (2)点B的坐标为(5,3).
【解析】
(1)设反比例函数的解析式为y=![]() ,把点A的横坐标代入直线解析式y=x-2,可求得点A的纵坐标,把点A的横纵坐标代入y=
,把点A的横坐标代入直线解析式y=x-2,可求得点A的纵坐标,把点A的横纵坐标代入y=![]() ,即可求得所求的反比例函数解析式;
,即可求得所求的反比例函数解析式;
(2)设点C(![]() ,m),则点B(m+2,m),根据BC=4列出方程m+2-
,m),则点B(m+2,m),根据BC=4列出方程m+2-![]() =4,解方程即可.
=4,解方程即可.
解:(1)设反比例函数的解析式为y=![]() .
.
∵横坐标为3的点A在直线y=x-2上,
∴y=3-2=1,
∴点A的坐标为(3,1),
∴1=![]() ,∴k=3,
,∴k=3,
∴反比例函数的解析式为y=![]() ;
;
(2)设点C(![]() ,m),则点B(m+2,m),
,m),则点B(m+2,m),
∵BC=4,
∴m+2-![]() =4,
=4,
∴m2+2m-3=4m,
∴m2-2m-3=0,
解得m1=3,m2=-1.
m1=3,m2=-1都是方程的解,但m=-1不符合题意,
∴点B的坐标为(5,3).

 名校课堂系列答案
名校课堂系列答案【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号 | 占地面积 (单位:m2/个) | 可供使用农户数 (单位:户/个) |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?