题目内容
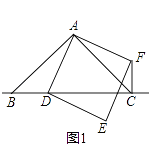
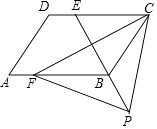
【题目】如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有 . (填序号) 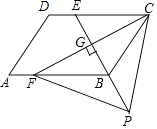
【答案】①②③④
【解析】解:证明:∵BC=EC,
∴∠CEB=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CEB=∠EBF,
∴∠CBE=∠EBF,
∴①BE平分∠CBF,正确;
∵BC=EC,CF⊥BE,
∴∠ECF=∠BCF,
∴②CF平分∠DCB,正确;
∵DC∥AB,
∴∠DCF=∠CFB,
∵∠ECF=∠BCF,
∴∠CFB=∠BCF,
∴BF=BC,
∴③正确;
∵FB=BC,CF⊥BE,
∴B点一定在FC的垂直平分线上,即PB垂直平分FC,
∴PF=PC,故④正确.
所以答案是①②③④.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目