题目内容
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示y关于x的函数关系的图象大致是( )
A.  B.
B. 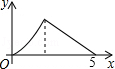 C.
C.  D.
D. 
B.
C.
解析试题分析:当点Q在AC上时,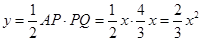 ;
;
当点Q在BC上时,
∵AP=x,AB=5,
∴BP=5﹣x,又cosB=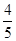 ,
,
∵△ABC∽QBP,
∴PQ=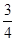 BP=
BP=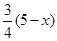
∴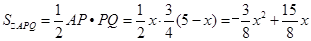 ,
,
∴该函数图象前半部分是抛物线开口朝上,后半部分也为抛物线开口向下.
故选C.
考点:动点问题.

练习册系列答案
相关题目
与y=2(x-1)2+3形状相同的抛物线解析式为( )
A.y=1+ x2 x2 | B.y=(2x+1)2 | C.y=(x-1)2 | D.y=2x2 |
将二次函数 化为
化为 的形式,结果为( )
的形式,结果为( )
A. | B.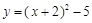 |
C. | D. |
若二次函数 配方后为
配方后为 ,则
,则 、
、 的值分别为( )
的值分别为( )
| A.8、-1 | B.8、1 | C.6、-1 | D.6、1 |
将抛物线y=3x2向右平移2个单位,则新抛物线的解析式是
A. | B. |
C. | D. |
抛物线y=2(x﹣3)2+1的顶点坐标是( )
| A.(3,1) | B.(3,﹣1) | C.(﹣3,1) | D.(﹣3,﹣1) |
如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系式中不正确的是( )
| A.h=m | B.n>h | C.k>n | D.h>0,k>0 |
 ,则这两个正方形的面积的和S关于
,则这两个正方形的面积的和S关于



 ,当x>0时,y随x的增大而增大,则二次函数
,当x>0时,y随x的增大而增大,则二次函数 的大致图象是( )
的大致图象是( )