��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У�A��B���������ֱ�ΪA��2��2����B��2����2�������ڸ������߶�AB����P��Q���������¶��壺����Q����AB����ֱ�ߵĶԳƵ�Q�����ڡ�ABP���ڲ��������߽磩����Ƶ�Q�ǵ�P�����߶�AB���ڳƵ㣮
��1����֪��P��4����1����
����Q1��1����1����Q2��1��1�������У��ǵ�P�����߶�AB���ڳƵ������ ����
������M��ֱ��y��x��1�ϣ��ҵ�M�ǵ�P�����߶�AB���ڳƵ㣬���M�ĺ�����xM��ȡֵ��Χ��
��2����֪��C��3��3������C�İ뾶Ϊr����D��4��0��������E�ǵ�D�����߶�AB���ڳƵ㣬������ֱ��DE����C���У���뾶r��ȡֵ��Χ��
���𰸡���1����Q1����0��xM��2����2��![]() ��r��
��r��![]() ��
��
��������
��1���������ڶԳƵ�����弴�ɵó����ۣ�
�����жϳ���O����ֱ��AB�ĶԳƵ�P'��ֱ��y��x��1�ϣ������жϳ����ۣ�
��2���жϳ�DE��ԲC����ʱ��ԲC���İ뾶����С��λ�ã����㼴�ɵó����ۣ�
�⣺��1����
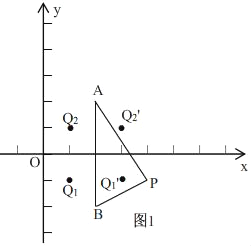
����ͼ�Σ����ڶԳƵ������ã���P�����߶�AB���ڳƵ����Q1��
�ʴ�ΪQ1��
����ͼ2��
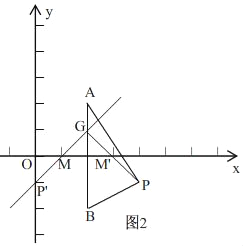
��P��4����1������AB����ֱ�ߵĶԳƵ�P'��0����1������ʱ����P'ǡ����ֱ��y��x��1�ϣ�
�ߵ�M�ǵ�P�����߶�AB���ڶԳƵ㣬
���M����AB����ֱ�ߵĶԳƵ�M'������ABP�ڲ��������߽磩��
�ߵ�M��ֱ��y��x��1�ϣ�
���MӦ���߶�P'G�ϣ���GΪ�߶�AB��ֱ��y��x��1�Ľ��㣩���Ҳ��������˵�P'��G�غϣ�
��0��xM��2��
��2����ͼ3��
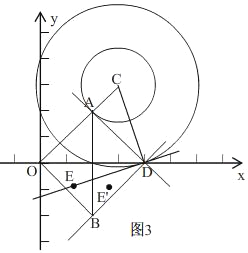
�ߵ�E�ǵ�D�����߶�AB���ڳƵ㣬
���E����AB����ֱ�ߵĶԳƵ�E'Ӧ����ABD�ڲ��������߽磩��
�ߵ�D����AB����ֱ�ߵĶԳƵ�Ϊԭ��O��
���EӦ����ABO���ڲ��������߽磩��
��A��2��2����C��3��3����D��4��0����
��AC��![]() ��AD��2
��AD��2![]() ��CD��
��CD��![]() ��
��
��AC2+AD2��CD2��
���CAD��90�㣬
��AC��AD��
��ʱ��ֱ��DA����ACΪ�뾶�ġ�C���У��뾶AC��![]() ��
��
��ֱ��DE����CDΪ�뾶�ġ�C���У���DΪ�е㣬��C�İ뾶������ֵΪ![]() ��
��
���������ġ�C�İ뾶r��ȡֵ��Χ��![]() ��r��
��r��![]() ��
��

 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�