题目内容
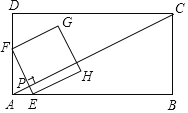
【题目】如图,在矩形ABCD中,AB=6![]() ,BC=3
,BC=3![]() 动点P从点A出发,沿AC以每秒4个单位长度的速度向终点C运动.过点P(不与点A、C重合)作EF⊥AC,交AB或BC于点E,交AD或DC于点F,以EF为边向右作正方形EFGH设点P的运动时间为t秒.
动点P从点A出发,沿AC以每秒4个单位长度的速度向终点C运动.过点P(不与点A、C重合)作EF⊥AC,交AB或BC于点E,交AD或DC于点F,以EF为边向右作正方形EFGH设点P的运动时间为t秒.
(1)①AC= .②当点F在AD上时,用含t的代数式直接表示线段PF的长 .
(2)当点F与点D重合时,求t的值.
(3)设方形EFGH的周长为l,求l与t之间的函数关系式.
(4)直接写出对角线AC所在的直线将正方形EFGH分成两部分图形的面积比为1:2时t的值.
【答案】(1)①15;②8t;(2)t=![]() ;(3)①当0<t≤
;(3)①当0<t≤![]() 时,l=40t;②当
时,l=40t;②当![]() <t≤3时,l=30;③当3<t<
<t≤3时,l=30;③当3<t<![]() 时,l=﹣40t+150;(4)t的值为
时,l=﹣40t+150;(4)t的值为![]() 或
或![]() .
.
【解析】
(1)①由矩形的性质和勾股定理即可得出结果;
②由矩形的性质得出∠D=90°,AD=BC=![]() ,CD=AB=
,CD=AB=![]() ,证明△APF∽△ADC,得出
,证明△APF∽△ADC,得出![]() ,即可得出结果;
,即可得出结果;
(2)当点F与点D重合时,证明△APD∽△ADC,得出![]() ,即可得出结果;
,即可得出结果;
(3)分情况讨论:
①当0<t≤![]() 时,由(1)②得:PF=8t,同理:PE=2t,得出EF=10t,即可得出结果;
时,由(1)②得:PF=8t,同理:PE=2t,得出EF=10t,即可得出结果;
②当![]() <t≤3时,EF=10t=
<t≤3时,EF=10t=![]() ,即可得出结果;
,即可得出结果;
③当3<t<![]() 时,同(1)①得:△CPF∽△ABC∽△EPC,得出
时,同(1)①得:△CPF∽△ABC∽△EPC,得出![]() ,得出PF=
,得出PF=![]() (15﹣4t),PE=2(15﹣4t),求出EF=PF+PE=
(15﹣4t),PE=2(15﹣4t),求出EF=PF+PE=![]() (15﹣4t)即可;
(15﹣4t)即可;
(4)由题意得出PE:PF=1:2,或PF:PE=1:2,①PE:PF=1:2时,得出PF=![]() EF=5,同理可证:△CPF∽△CDA,得出
EF=5,同理可证:△CPF∽△CDA,得出![]() ,即可得出结果;
,即可得出结果;
②PF:PE=1:2时,PF=![]() EF=
EF=![]() ,则
,则![]() (15﹣4t)=
(15﹣4t)=![]() ,解得:t=
,解得:t=![]() 即可.
即可.
解:(1)①∵四边形ABCD是矩形,
∴∠B=90°,
∴![]() ;
;
故答案为:15;
②∵四边形ABCD是矩形,
∴∠D=90°,AD=BC=3![]() ,CD=AB=6
,CD=AB=6![]() ,
,
∵EF⊥AC,
∴∠APF=90°=∠D,
∵∠PAF=∠DAC,
∴△APF∽△ADC,
∴![]() ,即
,即![]() ,
,
解得:PF=8t;
故答案为:8t;
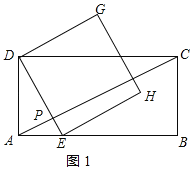
(2)当点F与点D重合时,如图1所示:
∵∠APD=∠ADC=90°,∠PAD=∠DAC,
∴△APD∽△ADC,
∴![]() ,即
,即![]() ,
,
解得:t=![]() ;
;
(3)分情况讨论:
①当0<t≤![]() 时,如图2所示:
时,如图2所示:
由(1)②得:PF=8t,
同理:PE=2t,
∴EF=10t,
∴l=4(8t+2t)=40t;
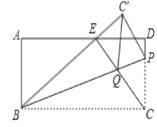
②当![]() <t≤3时,如图3所示:
<t≤3时,如图3所示:
EF=10t=![]() ,
,
l=4×![]() =30.
=30.
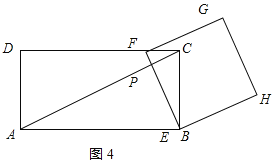
③当3<t<![]() 时,如图4所示:
时,如图4所示:
同(1)①得:△CPF∽△ABC∽△EPC,
∴![]()
即![]() ,
,
解得:PF=![]() (15﹣4t),PE=2(15﹣4t),
(15﹣4t),PE=2(15﹣4t),
∴EF=PF+PE=![]() (15﹣4t),
(15﹣4t),
∴l=4×![]() (15﹣4t)=﹣40t+150;
(15﹣4t)=﹣40t+150;
(4)如图3所示:对角线AC所在的直线将正方形EFGH分成两部分图形的面积比为1:2时,
则PE:PF=1:2,或PF:PE=1:2,
①PE:PF=1:2时,
∵EF=![]() ,
,
∴PF=![]() EF=5,
EF=5,
同理可证:△CPF∽△CDA,
∴![]() ,即
,即![]() ,
,
解得:PF=![]() (15﹣4t),
(15﹣4t),
∴![]() (15﹣4t)=5,
(15﹣4t)=5,
解得:t=![]() ;
;
②PF:PE=1:2时,PF=![]() EF=
EF=![]() ,
,
则![]() (15﹣4t)=
(15﹣4t)=![]() ,
,
解得:t=![]() ;
;
综上所述,对角线AC所在的直线将正方形EFGH分成两部分图形的面积比为1:2时t的值为![]() 或
或![]() .
.