Question

【题目】如图1，直线y=﹣ x+n交x轴于点A，交y轴于点C（0，4），抛物线y= x2+bx+c经过点A，交y轴于点B（0，﹣2）．点P为抛物线上一个动点，过点P作x轴的垂线PD，过点B作BD⊥PD于点D，连接PB，设点P的横坐标为m．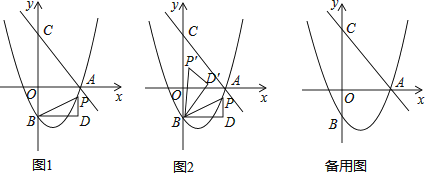
（1）求抛物线的解析式；
（2）当△BDP为等腰直角三角形时，求线段PD的长；
（3）如图2，将△BDP绕点B逆时针旋转，得到△BD′P′，且旋转角∠PBP′=∠OAC，当点P的对应点P′落在坐标轴上时，请直接写出点P的坐标．

Answer 1

【答案】
（1）

解：∵点C（0，4）在直线y=﹣ x+n上，

∴n=4，

∴y=﹣ x+4，

令y=0，

∴x=3，

∴A（3，0），

∵抛物线y= x2+bx+c经过点A，交y轴于点B（0，﹣2）．

∴c=﹣2，6+3b﹣2=0，

∴b=﹣ ，

∴抛物线解析式为y= x2﹣ x﹣2

（2）

解：点P为抛物线上一个动点，设点P的横坐标为m．

∴P（m， m2﹣ m﹣2），

∴BD=|m|，PD=| m2﹣ m﹣2+2|=| m2﹣ m|，

∵△BDP为等腰直角三角形，且PD⊥BD，

∴BD=PD，

∴|m|=| m2﹣ m|，

∴m=0（舍），m= ，m= ，

∴PD= 或PD=

（3）

解：∵∠PBP'=∠OAC，OA=3，OC=4，

∴AC=5，

∴sin∠PBP'= ，cos∠PBP'= ，

①当点P'落在x轴上时，过点D'作D'N⊥x轴，垂足为N，交BD于点M，

∠DBD'=∠ND'P'=∠PBP'，

如图1，

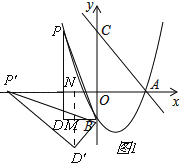
ND'﹣MD'=2，

∴ （ m2﹣ m）﹣（﹣ m）=2，

∴m= （舍），或m=﹣ ，

如图2，

ND'+MD'=2，

∴ （ m2﹣ m）+ m=2，

∴m= ，或m=﹣ （舍），

∴P（﹣ ， ）或P（ ， ），

②当点P'落在y轴上时，如图3，

过点D′作D′M⊥x轴，交BD于M，过P′作P′N⊥y轴，

∴∠DBD′=∠ND′P′=∠PBP′，

∵P′N=BM，

∴ （ m2﹣ m）= m，

∴m= ，

∴P（ ， ）．

∴P（﹣ ， ）或P（ ， ）或P（ ， ）

【解析】（1）先确定出点A的坐标，再用待定系数法求出抛物线解析式；
（2）由△BDP为等腰直角三角形，判断出BD=PD，建立m的方程计算出m，从而求出PD；
（3）分点P′落在x轴和y轴两种情况计算即可．