Question

【题目】如图①，在△ABC中，AC=BC，点D为BC的中点，DE⊥AB，垂足为点E，过点B作BG∥AC交DE的延长线于点G．
（1）求证：DB=BG；
（2）当∠ACB=90°时，如图②，连接AD、CG，求证：AD⊥CG．

Answer 1

【答案】
（1）证明：∵AC=BC，

∴∠A=∠CBA，

∵AC∥BG，

∴∠A=∠GBA，即∠CBA=∠GBA，

∵DE⊥AB，

∴∠DEB=∠GEB，

在△DBE和△GBE中

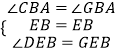
∴△DBE≌△GBE（ASA），

∴DB=BG；

（2）证明：∵点D为BC的中点，

∴CD=DB，

∵DB=BG，

∴CD=BG，

∵AC∥BG，

∴∠ACB+∠GBC=180°，

∵∠ACB=90°，

∴∠GBC=∠ACB=90°，

在△ACD和△CBG中

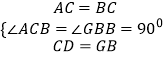
∴△ACD≌△CBG（SAS），

∴∠CAD=∠BCG，

∵∠ACG+∠BCG=90°，

∴∠ACG+∠CAD=90°，

即 AD⊥CG．

【解析】（1）由条件证明△DBE≌△GBE即可；（2）由条件可证明△ACD≌△CBG，再利用角的和差可证得结论．