Question

【题目】如图，AB∥CD，E 是直线 CD 上的一点，且 ∠BAE=30°， 是直线 CD 上的一动点，M是 AP 的中点，直线 MN⊥AP 且与 CD 交于点 N，设 ∠BAP=X°，∠MNE=Y°．

（1）在图2 中，当 x=12 时，∠MNE= ；在图 3 中，当 x=50 时，∠MNE= ；

（2）研究表明：y与x之间关系的图象如图4所示（ 不存在时，用空心点表示），请你根据图象直接估计当 y=100 时，x= ；

（3）探究：当 x= 时，点 N 与点 E 重合；

（4）探究：当 x>105 时，求y与x之间的关系式．

Answer 1

【答案】（1）102°，40°；(2)10或170；(3)15或105.（4）y=270-x

【解析】（1）当x=12时，根据三角形外角的性质可：∠MNE=90°+12°=102°；

当x=50°，根据直角三角形两锐角互余可得结论；

（2）由图象直接得出结论；

（3）分两种情况：①P在E的左侧，②P在E的右侧，根据平行线的性质和中垂线的性质可得结论；

（4）如图7，根据三角形外角和为360°列式可得结论．

解：（1）如图2，∵AB∥CD，

∴∠BAP=∠APN=x°，

∵MN⊥AP，

∴∠PMN=90°，

∴∠MNE=∠PMN+∠APN=90°+x°，

当x=12时，∠MNE=（90+12）°=102°；

即y=102°，

如图3中，当x=50时，∠APN=50°，

∴y=∠MNE=90°-x°=90°-50°=40°，

故答案为：102°，40°；

（2）如图2，当0＜x＜30时，y=90+x，

此时，y=100时，90+x=100，x=10，

由图4可知：y=100时，还有x=170，

∴当y=100时，x=10或170，

故答案为：10或170；

（3）①P在E的左侧时，当N与E重合时，如图5，∠BAE=∠AEP=30°，

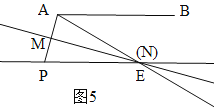
∵MN是AP的中垂线，

∴AE=PE，

∴∠AEM=∠PEM=15°，

∴∠EAP=90°-15°=75°，

∴∠BAP=x=30°+75°=105°，

②P在E的右侧时，当N与E重合时，如图6，

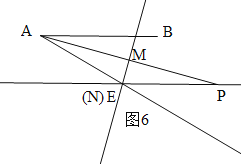
∵AB∥CD，

∴∠BAP=∠APE=x，

同理得：AE=PE，

∴∠EAM=∠EPM=x，

∵∠BAE=30°，

∴∠BAP=x=∠EAP=∠BAE=15°，

综上所述，当x=15或105时，点N与点E重合；

故答案为：15或105；

（4）当x＞105时，如图7，

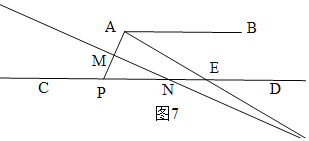
∵AB∥CD，

∴∠APC=∠BAP=x，

∵∠APC+∠MNE+∠AMN=360°，∠AMN=90°，

∴∠APC+∠MNE=360°-90°=270°，

∴∠MNE=270°-∠APC=270°-∠BAP，

即y=270-x．