题目内容
【题目】已知:如图,在山脚的C处测得山顶A的仰角为 ![]() ,沿着坡角为
,沿着坡角为 ![]() 的斜坡前进400米到D处(即
的斜坡前进400米到D处(即 ![]() ,
, ![]() 米),测得山顶A的仰角为
米),测得山顶A的仰角为 ![]() ,求山的高度AB.
,求山的高度AB.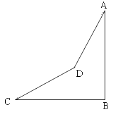
【答案】解:作DE⊥AB于E,作DF⊥BC于F,在RtΔCDF中,
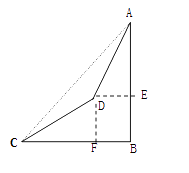
![]()
![]() =
= ![]() =200(米)
=200(米)
![]() =
= ![]() (米)
(米)
在 ![]() 中,
中, ![]() ,设DE=x米,
,设DE=x米,
∴ ![]() (米)
(米)
在矩形DEBF中,BE=DF=200米,
在 ![]() ,
,
∴AB=BC,
即: ![]()
∴x=200,
∴ ![]() 米
米
【解析】根据题意添加辅助线,作DE⊥AB于E,作DF⊥BC于F,在RtΔCDF中,由CD=400,根据30°角所对的直角边等于斜边的一半,求出DF的长,再求出CF的长,在RtΔADE中,设DE=x米,表示出AE的长,再证明DEBF是矩形,得出DE=BF,BE=DF,然后证明 △ACB是等腰直角三角形,得出AB=BC,建立关于x的方程,解方程,再根据AB=AE+BE,即可得出结果。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目




