题目内容
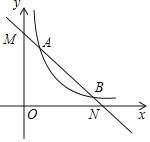
【题目】如图,已知AC=BC,点D是BC上一点,∠ADE=∠C.
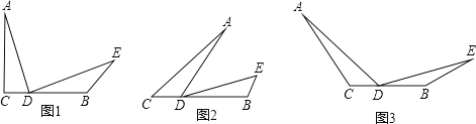
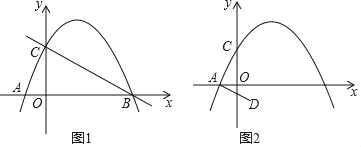
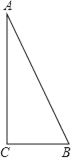
(1)如图1,若∠C=90°,∠DBE=135°.
①求证:∠EDB=∠CAD;
②求证:DA=DE;
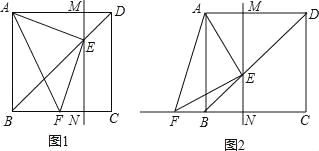
(2)如图2,若∠C=40°,DA=DE,求∠DBE的度数;
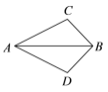
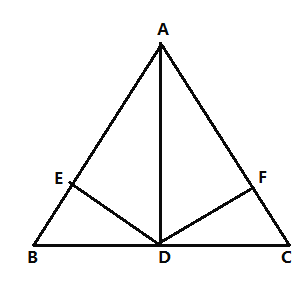
(3)如图3,请直接写出∠DBE与∠C之间满足什么数量关系时,总有DA=DE成立.
【答案】(1)①证明见解析;②证明见解析;(2)∠AGD=110°;(3)∠DBE=90°+![]() ∠C.
∠C.
【解析】
(1)①根据三角形的内角和及平角的定义可得结论;
②如图1,作辅助线,构建等腰直角三角形,利用ASA证明△AFD≌△DBE(ASA),可得结论;
(2)方法一:如图2,同理作辅助线,证明△AGD≌△DBE(SAS),得∠AGD=∠DBE=110°;
方法二:如图2,延长DB到点H使DH=AC,连接EH,证明△ACD≌△DHE(SAS),得∠C=∠H=40°,CD=EH,再根据已知证明CD=BH=EH,可得结论;
(3)同理作辅助线,证明△AFD≌△DBE(SAS),根据三角形的外角和三角形内角和定理可得结论.
(1)证明:①∵∠ADE=∠C,
∴∠CAD=180°-∠C-∠ADC,
∠EDB=180°-∠ADE-∠ADC,
∴∠CAD=∠EDB;
②在AC上截取CF=CD,连接FD,(或在AC上截取AF=BD,连接FD)
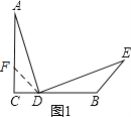
∵∠C=90°,
∴∠CFD=∠CDF=45°,
∴∠AFD=135°=∠DBE,
∵AC=BC,
∴AC-CF=BC-CD,即:AF=BD,
由①知:∠CAD=∠BDE,
∴△AFD≌△DBE(ASA),
∴DA=DE;
(2)方法一:如图2,在AC上截取AG=DB,连接GD(在AC上截取CG=CD,连接GD),
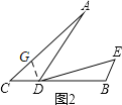
∵AC=BC,
∴AC-AG=BC-BD即:CG=CD,
∴∠CGD=∠CDG=![]() =70°,
=70°,
∵DA=DE,∠CAD=∠EDB(已证),AG=DB,
∴△AGD≌△DBE(SAS),
∴∠AGD=∠DBE=110°;
方法二:如图3,延长DB到点H使DH=AC,连接EH,

∵∠CAD=∠BDE,AD=DE,
∴△ACD≌△DHE(SAS),
∴∠C=∠H=40°,CD=EH,
∵AC=BC=DH,
∴CD=BH=EH,
∴∠HBE=∠HEB=70°,
∴∠DBE=110°;
(3)当∠DBE=90°+![]() ∠C时,总有DA=DE成立;
∠C时,总有DA=DE成立;
理由是:如图3,在AC上截取CF=CD,连接DF,则∠CDF=∠CFD,
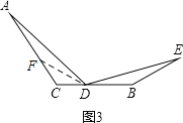
设∠CDF=x,
△CDF中,∠C+∠CDF+∠CFD=180°,
∴∠C+x+x=180°,
x=![]() =90°-
=90°-![]() ,
,
同理得△AFD≌△DBE(SAS),
∴∠AFD=∠DBE=∠C+∠CDF=∠C+x=∠C+90°-![]() ∠C,
∠C,
∴∠DBE=90°+![]() ∠C.
∠C.