题目内容
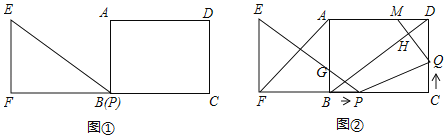
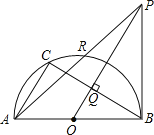
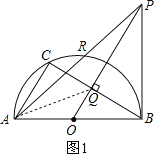
【题目】如图,AB是半圆O的直径,C是半圆O上一点,OQ⊥BC于点Q,过点B作半圆O的切线,交OQ的延长线于点P,PA交半圆O于R,则下列等式中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
(1)连接AQ,易证△OQB∽△OBP,得到![]() ,也就有
,也就有![]() ,可得△OAQ∽OPA,从而有∠OAQ=∠APO.易证∠CAP=∠APO,从而有∠CAP=∠OAQ,则有∠CAQ=∠BAP,从而可证△ACQ∽△ABP,可得
,可得△OAQ∽OPA,从而有∠OAQ=∠APO.易证∠CAP=∠APO,从而有∠CAP=∠OAQ,则有∠CAQ=∠BAP,从而可证△ACQ∽△ABP,可得![]() ,所以A正确.
,所以A正确.
(2)由△OBP∽△OQB得![]() ,即
,即![]() ,由AQ≠OP得
,由AQ≠OP得![]() ,故C不正确.
,故C不正确.
(3)连接OR,易得![]() ,
,![]() ,得到
,得到![]() ,故B不正确.
,故B不正确.
(4)由![]() 及AC=2OQ,AB=2OB,OB=OR可得
及AC=2OQ,AB=2OB,OB=OR可得![]() ,由AB≠AP得
,由AB≠AP得![]() ,故D不正确.
,故D不正确.
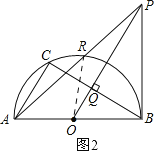
解:(1)连接AQ,如图1,
∵BP与半圆O切于点B,AB是半圆O的直径,
∴∠ABP=∠ACB=90°.
∵OQ⊥BC,
∴∠OQB=90°.
∴∠OQB=∠OBP=90°.
又∵∠BOQ=∠POB,
∴△OQB∽△OBP.
∴![]() .
.
∵OA=OB,
∴![]() .
.
又∵∠AOQ=∠POA,
∴△OAQ∽△OPA.
∴∠OAQ=∠APO.
∵∠OQB=∠ACB=90°,
∴AC∥OP.
∴∠CAP=∠APO.
∴∠CAP=∠OAQ.
∴∠CAQ=∠BAP.
∵∠ACQ=∠ABP=90°,
∴△ACQ∽△ABP.
∴![]() .
.
故A正确.
(2)如图1,
∵△OBP∽△OQB,
∴![]() .
.
∴![]() .
.
∵AQ≠OP,
∴![]() .
.
故C不正确.
(3)连接OR,如图2所示.
∵OQ⊥BC,
∴BQ=CQ.
∵AO=BO,
∴OQ=![]() AC.
AC.
∵OR=![]() AB.
AB.
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
故B不正确.
(4)如图2,
∵![]() ,
,
且AC=2OQ,AB=2OB,OB=OR,
∴![]() .
.
∵AB≠AP,
∴![]() .
.
故D不正确.
故选:A.

 举一反三期末百分冲刺卷系列答案
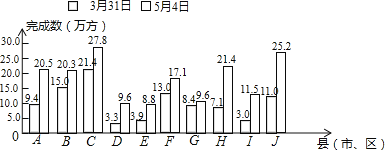
举一反三期末百分冲刺卷系列答案【题目】在全体丽水人民的努力下,我市剿灭劣V类水“河道清淤”工程取得了阶段性成果,如表是全市十个县(市、区)指标任务数的统计表;如图是截止2017年3月31日和截止5月4日,全市十个县(市、区)指标任务累计完成数的统计图.
全市十个县(市、区)指标任务数统计表
县(市、区) | 任务数(万方) |
A | 25 |
B | 25 |
C | 20 |
D | 12 |
E | 13 |
F | 25 |
G | 16 |
H | 25 |
I | 11 |
J | 28 |
合计 | 200 |
(1)截止3月31日,完成进度(完成进度=累计完成数÷任务数×100%)最快、最慢的县(市、区)分别是哪一个?
(2)求截止5月4日全市的完成进度;
(3)请结合图表信息和数据分析,对Ⅰ县完成指标任务的行动过程和成果进行评价.