ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЌЧв
ЮЊГЃЪ§ЃЌЧв![]() ЃЉгы
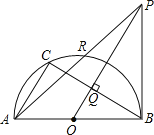
ЃЉгы![]() жсДгзѓжСгввРДЮНЛгкA,BСНЕуЃЌгы
жсДгзѓжСгввРДЮНЛгкA,BСНЕуЃЌгы![]() жсНЛгкЕуCЃЌОЙ§ЕуBЕФжБЯп
жсНЛгкЕуCЃЌОЙ§ЕуBЕФжБЯп![]() гыХзЮяЯпЕФСэвЛНЛЕуЮЊD.
гыХзЮяЯпЕФСэвЛНЛЕуЮЊD.
ЃЈ1ЃЉШєЕуDЕФКсзјБъЮЊ-5ЃЌЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєдкЕквЛЯѓЯоЕФХзЮяЯпЩЯгаЕуPЃЌЪЙЕУвдAЃЌBЃЌPЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЩшFЮЊЯпЖЮBDЩЯвЛЕуЃЈВЛКЌЖЫЕуЃЉЃЌСЌНгAFЃЌвЛЖЏЕуMДгЕуAГіЗЂЃЌбиЯпЖЮAFвдУПУы1ИіЕЅЮЛЕФЫйЖШдЫЖЏЕНFЃЌдйбиЯпЖЮFDвдУПУы2ИіЕЅЮЛЕФЫйЖШдЫЖЏЕНDКѓЭЃжЙ. ЕБЕуFЕФзјБъЪЧЖрЩйЪБЃЌЕуMдкећИідЫЖЏЙ§ГЬжагУЪБзюЩйЃП

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉF
ЃЛЃЈ3ЃЉF![]() .
.
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉИљОнЕудкЧњЯпЩЯЕуЕФзјБъТњзуЗНГЬЕФЙиЯЕЃЌвРДЮЧѓГі![]() ЕФжЕЕУЕНжБЯпЕФНтЮіЪНЁЂЕуDЕФзнзјБъЁЂ
ЕФжЕЕУЕНжБЯпЕФНтЮіЪНЁЂЕуDЕФзнзјБъЁЂ![]() ЕФжЕЕУЕНХзЮяЯпЕФКЏЪ§БэДяЪН.
ЕФжЕЕУЕНХзЮяЯпЕФКЏЪ§БэДяЪН.
ЁпBM=9ЃЌAB=6ЃЌЁрBF=![]() ЃЌBD=
ЃЌBD=![]() ЃЌAF=
ЃЌAF=![]()
ЃЈ2ЃЉЗжЁїPABЁзЁїABCКЭЁїPABЁзЁїBACСНжжЧщПіЬжТлМДПЩ.
ЃЈ3ЃЉЙ§ЕуDзїDHЁЭyжсгкЕуHЃЌЙ§ЕуAзїAGЁЭDHгкЕуGЃЌНЛBDгкЕуFЃЌдђЕуFМДЮЊЫљЧѓЃЌРэгЩЪЧЃЌгЩгкЕуMдкЯпЖЮAFЩЯвдУПУы1ИіЕЅЮЛЕФЫйЖШдЫЖЏЃЌдкЯпЖЮFDЩЯвдУПУы2ИіЕЅЮЛЕФЫйЖШдЫЖЏЃЌДгЖјИљОнжБЯпBDЕФЧуаБНЧЪЧ30ЁужЊЕР![]() ЃЌгжИљОнДЙжБЯпЖЮзюЖЬЕФаджЪжЊЕуFМДЮЊЫљЧѓЃЌДгЖјИљОнКЌ30ЁужБНЧШ§НЧаЮЕФаджЪЧѓНтМДПЩ.
ЃЌгжИљОнДЙжБЯпЖЮзюЖЬЕФаджЪжЊЕуFМДЮЊЫљЧѓЃЌДгЖјИљОнКЌ30ЁужБНЧШ§НЧаЮЕФаджЪЧѓНтМДПЩ.
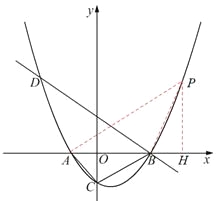
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпХзЮяЯп![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЌЧв
ЮЊГЃЪ§ЃЌЧв![]() ЃЉгы
ЃЉгы![]() жсДгзѓжСгввРДЮНЛгкA,BСНЕуЃЌ
жсДгзѓжСгввРДЮНЛгкA,BСНЕуЃЌ
ЁрAЃЈ-2ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉ.
ЁпЕуBдкжБЯп![]() ЩЯЃЌЁр
ЩЯЃЌЁр![]() ЃЌМД
ЃЌМД![]() .
.
ЁржБЯпЕФНтЮіЪНЮЊ![]() .
.
ЁпЕуDдкжБЯп![]() ЩЯЃЌЧвКсзјБъЮЊ-5ЃЌЁрзнзјБъЮЊ
ЩЯЃЌЧвКсзјБъЮЊ-5ЃЌЁрзнзјБъЮЊ![]() .
.
ЁпЕуDдкХзЮяЯп![]() ЩЯЃЌЁр
ЩЯЃЌЁр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() .
.
ЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊ![]() .
.
ЃЈ2ЃЉвзЕУЃЌЕуCЕФзјБъЮЊ![]() ЃЌдђ
ЃЌдђ![]() .
.
ЩшЕуPЕФзјБъЮЊ![]() ЃЌ
ЃЌ
ЗжСНжжЧщПіЃК
ЂйШєЁїPABЁзЁїABCЃЌдђЁЯPAB=ЁЯABCЃЌ![]() .
.
ЁргЩЁЯPAB=ЁЯABC ЕУ![]() ЃЌМД
ЃЌМД![]() .
.
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() .
.
ДЫЪБЕуPЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁргЩ![]() ЕУ
ЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() .
.
ЂкШєЁїPABЁзЁїBACЃЌдђЁЯPAB=ЁЯBACЃЌ![]() .
.
ЁргЩЁЯPAB=ЁЯBAC ЕУ![]() ЃЌМД
ЃЌМД![]() .
.
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() .
.
ДЫЪБЕуPЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁргЩ![]() ЕУ
ЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() .
.
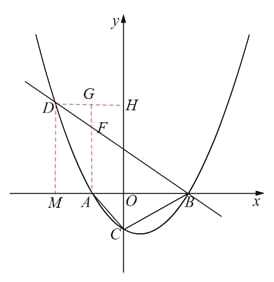
ЃЈ3ЃЉШчЭМЃЌЙ§ЕуDзїDHЁЭyжсгкЕуHЃЌЙ§ЕуAзїAGЁЭDHгкЕуGЃЌНЛBDгкЕуFЃЌдђЕуFМДЮЊЫљЧѓ.
ЁпжБЯпBDЕФНтЮіЪНЮЊ![]() ЃЌЁрЁЯFBA=ЁЯFGD=30Ёу.
ЃЌЁрЁЯFBA=ЁЯFGD=30Ёу.
ЁпAB=6ЃЌЁрAF=![]() .
.
ЁрЕуFЕФзјБъЮЊ![]() .
.

ЁОЬтФПЁПФГЦЗХЦЪжЛњШЅФъУПЬЈЕФЪлМлyЃЈдЊЃЉгыдТЗнxжЎМфТњзуКЏЪ§ЙиЯЕЃКyЃНЉ50x+2600ЃЌШЅФъЕФдТЯњСПpЃЈЭђЬЈЃЉгыдТЗнxжЎМфГЩвЛДЮКЏЪ§ЙиЯЕЃЌЦфжа1Љ6дТЗнЕФЯњЪлЧщПіШчЯТБэЃК
дТЗнЃЈxЃЉ | 1дТ | 2дТ | 3дТ | 4дТ | 5дТ | 6дТ |
ЯњЪлСПЃЈpЃЉ | 3.9ЭђЬЈ | 4.0ЭђЬЈ | 4.1ЭђЬЈ | 4.2ЭђЬЈ | 4.3ЭђЬЈ | 4.4ЭђЬЈ |
ЃЈ1ЃЉЧѓpЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓИУЦЗХЦЪжЛњдкШЅФъФФИідТЕФЯњЪлН№ЖюзюДѓЃПзюДѓЪЧЖрЩйЭђдЊЃП
ЃЈ3ЃЉНёФъ1дТЗнИУЦЗХЦЪжЛњЕФЪлМлБШШЅФъ12дТЗнЯТНЕСЫm%ЃЌЖјЯњЪлСПвВБШШЅФъ12дТЗнЯТНЕСЫ1.5m%ЃЎНёФъ2дТЗнЃЌОЯњЩЬОіЖЈЖдИУЪжЛњвд1дТЗнМлИёЕФЁААЫелЁБЯњЪлЃЌетбљ2дТЗнЕФЯњЪлСПБШНёФъ1дТЗндіМгСЫ1.5ЭђЬЈЃЎШєНёФъ2дТЗнетжжЦЗХЦЪжЛњЕФЯњЪлЖюЮЊ6400ЭђдЊЃЌЧѓmЕФжЕЃЎ