题目内容
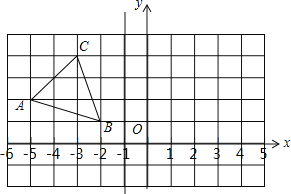
【题目】在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形上)
(1)画出△ABC关于直线l:x=﹣1的对称三角形△A1B1C1;并写出A1、B1、C1的坐标.
(2)在直线x=﹣l上找一点D,使BD+CD最小,满足条件的D点为 .
提示:直线x=﹣l是过点(﹣1,0)且垂直于x轴的直线.
【答案】(1)A1(3,1),B1(0,0),C1(1,3);见解析;(2)(﹣1,1).
【解析】
试题分析:(1)分别作出点A、B、C关于直线l:x=﹣1的对称的点,然后顺次连接,并写出A1、B1、C1的坐标;
(2)作出点B关于x=﹣1对称的点B1,连接CB1,与x=﹣1的交点即为点D,此时BD+CD最小,写出点D的坐标.
解:(1)所作图形如图所示:
A1(3,1),B1(0,0),C1(1,3);
(2)作出点B关于x=﹣1对称的点B1,
连接CB1,与x=﹣1的交点即为点D,
此时BD+CD最小,
点D坐标为(﹣1,1).
故答案为:(﹣1,1).


练习册系列答案
相关题目