Question

【题目】如图，在菱形ABCD中，AB＝6，∠DAB＝60°，AE分别交BC，BD于点E，F，CE＝2，连接CF．给出以下结论：①△ABF≌△CBF；②点E到AB的距离是3；③tan∠DCF＝；④△ABF的面积为．其中正确的结论序号是_____

Answer 1

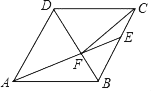
【答案】①②③④

【解析】

利用SAS证明△ABF与△CBF全等，得出①正确，根据含30°角的直角三角形的性质得出点E到AB的距离是2，得出②错误，同时求出△ABF的面积，得出④错误，得出tan∠DCF＝，得出③正确．

解：∵四边形ABCD是菱形，

∴AB＝BC＝6，

∵∠DAB＝60°，

∴AB＝AD＝DB，∠ABD＝∠DBC＝60°，

在△ABF与△CBF中，

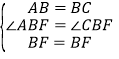
∴△ABF≌△CBF（SAS），故①正确；

过点E作EG⊥AB，过点F作MH⊥CD于M，MH⊥AB于H，如图所示：

∵CE＝2，BC＝6，∠ABC＝120°，

∴BE＝6﹣2＝4，

∵EG⊥AB，

∴EG＝2，

∴点E到AB的距离是2，故②错误；

∵BE＝4，EC＝2，

∴S△BFE：S△FEC＝4：2＝2：1，

∴S△ABF：S△FBE＝3：2，

∴△ABF的面积为＝S△ABE＝××6×2＝，故④正确；

∵S△ADB＝×6×3＝9，

∴S△DFC＝S△ADB﹣S△ABF＝9﹣＝，

∵S△DFC＝×6×MF，

∴FM＝，

∴DM＝=，

∴CM＝DC﹣DM＝6﹣＝，

∴tan∠DCF＝＝，

故③正确；

故答案为：①②③④