题目内容
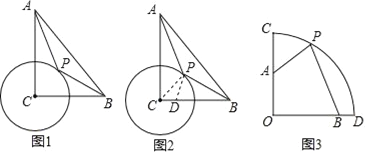
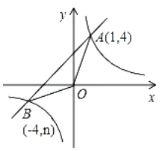
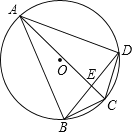
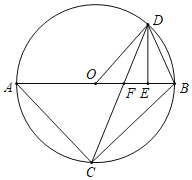
【题目】如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC.设△DOE的面积为S.sinA=![]() ,求四边形BCOD的面积(用含有S的式子表示)
,求四边形BCOD的面积(用含有S的式子表示)
【答案】(1)见解析;(2)见解析;(3)S四边形BCOD=![]() .
.
【解析】
(1)根据圆周角定理和垂直(DE⊥AB)得出∠DEO=∠ACB;根据平行(OD∥BC)得出∠DOE=∠ABC;根据相似三角形的判定即可证明;
(2)根据相似三角形的性质可得∠ODE=∠A,根据圆周角定理可得∠A=∠BDC,进而推出∠ODE=∠BDC,等式两边同时减去∠EDF即可证明∠ODF=∠BDE.
(3)根据相似三角形的性质可得S△ABC=4S△DOE=4S,进而可得S△BOC=2S;由sinA=![]() ,∠A=∠ODE及圆的半径相等(OD=OB),可得
,∠A=∠ODE及圆的半径相等(OD=OB),可得![]() ,将三部分的面积相加,即可解答本题.
,将三部分的面积相加,即可解答本题.
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
(2)证明:∵△DOE∽△ABC,
∴∠ODE=∠A,
∵∠A和∠BDC是![]() 所对的圆周角,
所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(3)解:∵△DOE∽△ABC,
∴![]() ,
,
即S△ABC=4S△DOE=4S,
∵OA=OB,
∴![]() ,
,
即S△BOC=2S,
∵sinA=![]() ,sinA=sin∠ODE,
,sinA=sin∠ODE,
∴![]() ,
,
∴OE=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴S四边形BCOD=S△BOC+S△DOE+![]() .
.

练习册系列答案
相关题目