题目内容
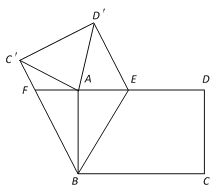
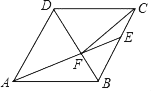
【题目】如图,E,F是平行四边形ABCD对角线BD上的两点,DE=EF=BF,连接CE并延长交AD于点G,连接CF并延长交AB于点H,连接CH,设△CDG的面积为S1,△CHG的面积为S2,则S1与S2的关系正确的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
首先根据平行四边形的性质和题干中的数量关系,可证明点G,H分别是AD,AB的中点;进而得到S1=S△CDG=S△BCH=![]() SABCD;再根据△AGH与△ADB的相似关系,可证得S△AGH=
SABCD;再根据△AGH与△ADB的相似关系,可证得S△AGH=![]() S△ABC=
S△ABC=![]() SABCD,通过SABCD、S△AGH、S△CDG、S△BCH的数量关系,可将S2表示为S2=
SABCD,通过SABCD、S△AGH、S△CDG、S△BCH的数量关系,可将S2表示为S2=![]() SABCD,对比S1
SABCD,对比S1![]() SABCD,最终可得S1与S2的关系.
SABCD,最终可得S1与S2的关系.
∵DE=EF=BF,
∴DF=2BF,BE=2DE
∵四边形ABCD是平行四边形
∴AD∥BC,AB∥CD,AB=CD,AD=BC
∴![]() ,
,![]()
∴CD=2HB,BC=2DG
∴点G,H分别是AD,AB的中点,
∴S1=S△CDG=S△BCH=![]() SABCD,GH∥DB
SABCD,GH∥DB
∵GH∥DB
∴△AGH∽△ADB
∴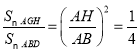
∴S△AGH=![]() S△ABC=
S△ABC=![]() SABCD,
SABCD,
∵S△CHG=SABCD-S△AGH-S△CDG-S△BCH,
∴S2=S△CHG=![]() SABCD,
SABCD,
∴S1=![]() S2,
S2,
故选:C.

练习册系列答案
相关题目