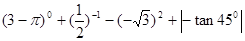题目内容
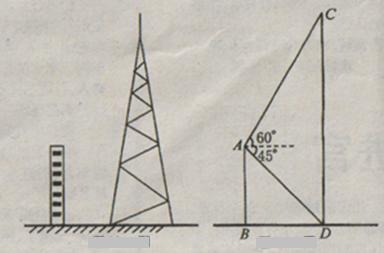
如图所示,我班同学组织课外实践活动,预测量一建筑物的高度,在建筑物附近一斜坡A点测得建筑物顶端D的仰角为30°,在坡底C点测得建筑物顶端D的仰角为60°,已知A点的高度AB为20米,AC的坡度为1∶1 (即AB∶BC=1∶1),且B、C、E三点在同一条直线上,请根据以上条件求出建筑物DE的高度(测量器的高度忽略不计). 

30+10

如图,过点A作AF⊥DE于F 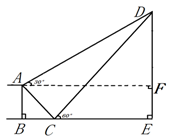
则四边形ABEF为矩形。
∴AF=BE EF="AB=20."
设 DE为x
在直角三角形CDE中,CE=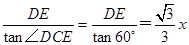 ……………2分
……………2分
在直角三角形ABC中,BC=AB=20 ………………………4分
在直角三角形AFD中,DF=AF tan30°=
tan30°=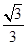 (BC+CE)=
(BC+CE)=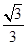 (20+
(20+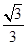 x)
x)
…………………………6分
∴DE=DF+FE=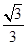 (20+
(20+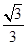 x)+20=x
x)+20=x
解方程得 x=30+10 (米) …………………………………7分
(米) …………………………………7分
答:建筑物的高度为30+10 米 …………………………………8分
米 …………………………………8分
利用三角函数求出CE、DF的长,设 DE为x,列方程求解

则四边形ABEF为矩形。
∴AF=BE EF="AB=20."
设 DE为x
在直角三角形CDE中,CE=
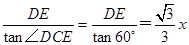 ……………2分
……………2分在直角三角形ABC中,BC=AB=20 ………………………4分
在直角三角形AFD中,DF=AF
 tan30°=
tan30°=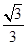 (BC+CE)=
(BC+CE)=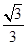 (20+
(20+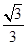 x)
x) …………………………6分
∴DE=DF+FE=
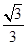 (20+
(20+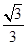 x)+20=x
x)+20=x 解方程得 x=30+10
 (米) …………………………………7分
(米) …………………………………7分 答:建筑物的高度为30+10
 米 …………………………………8分
米 …………………………………8分 利用三角函数求出CE、DF的长,设 DE为x,列方程求解

练习册系列答案
相关题目
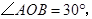 过
过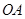 上到点
上到点 的距离为1,3,5,7,…的点作
的距离为1,3,5,7,…的点作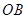 相交,得到图所示的阴影梯形,它们的面积依次记为
相交,得到图所示的阴影梯形,它们的面积依次记为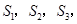 ….则
….则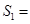 ;通过计算可得
;通过计算可得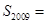
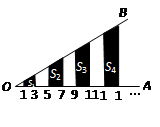
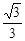 )米,又知在A处观测山顶P的仰角为45°,求AB两地的距离及小山的高(结果保留根号).
)米,又知在A处观测山顶P的仰角为45°,求AB两地的距离及小山的高(结果保留根号).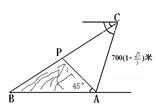

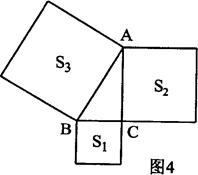
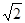 ≈1.414,
≈1.414,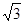 ≈1.732)
≈1.732)
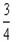 ,则sinA=______
,则sinA=______