题目内容
【题目】如图,抛物线y=x2+bx+ ![]() 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 . 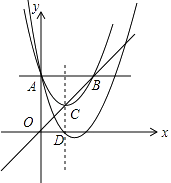
【答案】y=x2﹣ ![]() x+
x+ ![]()
【解析】解:∵令x=0,则y= ![]() , ∴点A(0,
, ∴点A(0, ![]() ),
),
根据题意,点A、B关于对称轴对称,
∴顶点C的纵坐标为 ![]() ×
× ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得b1=3,b2=﹣3,
由图可知,﹣ ![]() >0,
>0,
∴b<0,
∴b=﹣3,
∴对称轴为直线x=﹣ ![]() =
= ![]() ,
,
∴点D的坐标为( ![]() ,0),
,0),
设平移后的抛物线的解析式为y=x2+mx+n,
则  ,
,
解得 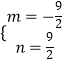 ,
,
所以,y=x2﹣ ![]() x+
x+ ![]() .
.
所以答案是:y=x2﹣ ![]() x+
x+ ![]() .
.
【考点精析】关于本题考查的二次函数图象的平移,需要了解平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能得出正确答案.

练习册系列答案
相关题目
【题目】小明本学期的数学测验成绩如表所示:
测验 类别 | 平时测验 | 期中 测验 | 期末 测验 | |||
第1次 | 第2此 | 第3次 | 第4次 | |||
成绩 | 80 | 86 | 84 | 90 | 90 | 95 |
(1)求六次测验成绩的众数和中位数;
(2)求小明本学期的数学平时测验的平均成绩;
(3)如果本学期的总评成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照3:3:4的比例计算所得,计算小明本学期学科的总评成绩。