题目内容
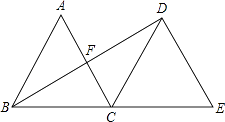
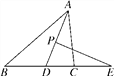
【题目】如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E,当P点在线段AD上运动时,∠E与∠B,∠ACB的数量关系为________________.
【答案】∠E=![]() (∠ACB-∠B)
(∠ACB-∠B)
【解析】由三角形的内角和为180°,AD是角平分线,可以用∠ABE和∠ACB表示∠BAD;仔细观察图形,∠PDE是△ABD的外角,由三角形外角定理可以用∠ABE、∠ACB表示出∠PDE,又求出了∠E与∠PDE互余,即可解答本题.
∵在△ABC中, ∠BAC=180°-(∠B+∠ACB),AD平分∠BAC,
∴∠BAD=90°-![]() (∠B+∠ACB).
(∠B+∠ACB).
∵∠ADC是△ABD的一个外角,
∴∠ADC=∠BAD+∠ABE=90°-![]() (∠B+∠ACB)+∠B=90°+
(∠B+∠ACB)+∠B=90°+![]() (∠B-∠ACB).
(∠B-∠ACB).
∵PE⊥AD,∠ADC=90°+![]() (∠B-∠ACB),
(∠B-∠ACB),
∴∠E=90°-[90°+![]() (∠B-∠ACB)]=
(∠B-∠ACB)]=![]() (∠ACB-∠B).
(∠ACB-∠B).
故答案为:∠E=![]() (∠ACB-∠B).
(∠ACB-∠B).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目