题目内容
【题目】在等边△ABC所在平面内找出一个点,使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形。这样的点一共有( )
A. 1个 B. 4个 C. 7个 D. 10个
【答案】D
【解析】
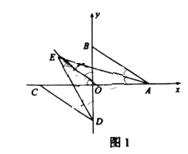
在等边△ABC中,三条边上的高交于点O,
由于等边三角形是轴对称图形,三条高所在的直线也是对称轴,也是边的中垂线,点O到三个顶点的距离相等,△ADB,△BOC,△AOC是等腰三角形,则点O是满足题中要求的点,
高与顶角的两条边成的锐角为30°,以点A为圆心,AB为半径,做圆,延长AO交圆于点E,
由于点E在对称轴AE上,有EC=EB,AE=AC=AB,△ECB,△AEC,△ABE都是等腰三角形,点E也是满足题中要求的点,
作AD⊥AB交圆于点D,则有AC=AD,AD=AB,即△DAB,△ADC是等腰三角形,点D也是满足题中要求的点,同理,作AF⊥AC交圆于点F,则点F也是满足题中要求的点;
同理,以点B为圆心,AB为半径,做圆,
以点C为圆心,AB为半径,做圆,都可以分别得到同样性质的三个点满足题中要求,
于是共有10个点能使点与三角形中的任意两个顶点所组成的三角形都是等腰三角形.
故选D.

【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元/公里计算,耗时费按
元/公里计算,耗时费按![]() 元/分钟计算(总费用不足
元/分钟计算(总费用不足![]() 元按
元按![]() 元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
里程数 | 耗时 | 车费(元) | |
小敏 |
|
|
|
小刚 |
|
|
|
![]() 求
求![]() 的值;
的值;
![]() 若小华也用该打车方式打车,平均车速为
若小华也用该打车方式打车,平均车速为![]() 公里/时,行驶了
公里/时,行驶了![]()
【题目】我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
根据以上信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你分别选择其中一个统计量作为选定标准,找出这10名男生中具有“普通身高”的是哪几位男生?并说明理由.
男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
身高x(cm) | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |