题目内容
【题目】探究题．
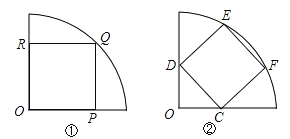
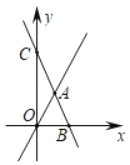
如图，
、
分别为数轴上的两点，点对应的数为
，点对应的数为
．
（
）请写出与、两点距离相等的点
所对应的数．
（
）现有一只电子蚂蚁
从点出发，以
单位/秒的速度向左运动，同时另一只电子蚂蚁
恰好从点出发，以
单位/秒的速度向右运动，设两只电子蚂蚁在数轴上的
点相遇，你知道点对应的数是多少吗？
（
）若当电子蚂蚁从点出发时，以单位/秒的速度向左运动，同时另一只电子蚂蚁恰好从点出发，以单位/秒的速度也向左运动，设两只电子蚂蚁在数轴上的
点相遇，你知道点对应的数是多少吗？
【答案】（1）40；（2）28；（3）-260
【解析】
(1)求-20与100和的一半即是M；
(2)此题是相遇问题,先求出相遇所需的时间,再求出点Q走的路程，根据“左减右加”的原则，可求出-20向右运动到相遇地点所对应的数；
(3)此题是追及问题,可先求出P追上Q所需的时间，然后可求出Q所走的路程，根据“左减右加”的原则，可求出点D所对应的数。
因为A、B分别是数轴上的两点，
点对应的数为
，
点对应的数为
则AB中点M对应的数是100-60=40
即M点对应的数是40；
(2)由题意知P与Q的相遇时间是
所以相同时间Q点运动的路程为
即从数-20向右运动48个单位到数28；
(3) P点追到Q点的时间为
所以此时Q点起过路程为
即从数-20向左运动240个单位到数-260.
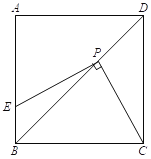
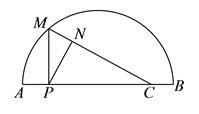
【题目】如图，点
，
之间有一条曲线和一条线段，
在线段
上，己知
，
，
是线段
上一动点，过点作
交曲线于点
，连接
，过点作
于点
．设，两点间的距离为
，，两点间的距离为
．（当点与点重合时，
的值为
）小思根据学习函数的经验，对函数随自变量
的变化而变化的规律进行了探究．
下面是小思的探究过程，请补充完整：
（
）通过取点，画图，测量，得到了与的几组值，补全下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（说明：补全表格时相关数值保留一位小数）
（
）在下列平面直角坐标系中描出以补全后的表中各对对应值为坐标的点，画出该函数的图象．
（
）结合画出的函数图象，解决问题：当
时，
的长度约为__________
（结果保留一位小数）．
