题目内容
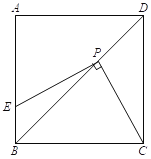
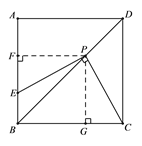
【题目】如图,正方形ABCD的边长为6,点E是边AB上一点,点P是对角线BD上一点,且PE⊥PC.
⑴ 求证:PC=PE;
⑵ 若BE=2,求PB的长.
【答案】(1)证明见解析;(2)![]()
【解析】分析: ![]() 过点P作PF⊥AB,PG⊥BC,垂足分别为点F、G.证明△PFE≌△PGC即可.
过点P作PF⊥AB,PG⊥BC,垂足分别为点F、G.证明△PFE≌△PGC即可.
![]() 设EF=x.根据 △PFE≌△PGC .得到GC=EF=x. 由BE=2得:BF=x+2.
设EF=x.根据 △PFE≌△PGC .得到GC=EF=x. 由BE=2得:BF=x+2.
由正方形FBGP得:BG=x+2. BG+GC=6.列出方程,求出![]() ,在△PFB中,用勾股定理即可求出PB的长.
,在△PFB中,用勾股定理即可求出PB的长.
详解:⑴ 过点P作PF⊥AB,PG⊥BC,垂足分别为点F、G.
∴ ∠PFB=∠PGB=∠PGC=90°,
∵ 四边形ABCD是正方形,
∴ ∠A=∠ABC=90°,AB=AD=BC,
∴ ∠ABD=∠ADB=45°,四边形FBGP是矩形,
∴ ∠FPB=90°-∠ABD=90°-45°=45°,
∴ ∠ABD=∠FPB,
∴ FP=FB,
∴ 矩形FBGP是正方形,
∴ PF=PG,∠FPG=90°,
∴ ∠FPG+∠EPG=90°,
∵ EP⊥PC,
∴ ∠EPC=90°,
∴ ∠GPC+∠EPG=90°,
∴ ∠FPG=∠GPC ,
∵ ∠FPG=∠GPC ,PF=PG,∠PFE=∠PGC,
∴△PFE≌△PGC(ASA)
∴ PE=PC.
 (方法不唯一,酌情给分)
(方法不唯一,酌情给分)
⑵ 设EF=x.
∵ △PFE≌△PGC .
∴ GC=EF=x.
由BE=2得:BF=x+2.
由正方形FBGP得:BG=x+2.
∵ BC=6,
∴ BG+GC=6.
∴ (x+2)+x=6,
解得:x=2.
∴ PF=BF=2+2=4 ,
△PFB中,∠PFB=90°,由勾股定理得: ![]() ,
,
∵ PB>0
∴![]()
答:PB的长为![]()

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目