题目内容
已知a,b,c是△ABC的三条边长,且关于x的方程(c-b)x2+2(b-a)x+(a-b)=0有两个相等的实数根,那么这个三角形是( )
A.等边三角形
B.等腰三角形
C.不等边三角形
D.直角三角形
【答案】分析:根据根的判别式△=b2-4ac=0及等腰三角形的判定解答.
解答:解:∵关于x的方程(c-b)x2+2(b-a)x+(a-b)=0有两个相等的实数根,
∴△=4(b-a)2-4(c-b)(a-b)=0,即(b-a)(c-a)=0,
∴b-a=0或c-a=0,解得b=a或c=a;
∵a,b,c 是△ABC的三条边长,
∴△ABC是等腰三角形;
故选B.
点评:本题主要考查了根的判别式、等腰三角形的判定.若关于其中一个未知数的一元二次方程有两个相等的实数根,则根的判别式△=0.
解答:解:∵关于x的方程(c-b)x2+2(b-a)x+(a-b)=0有两个相等的实数根,
∴△=4(b-a)2-4(c-b)(a-b)=0,即(b-a)(c-a)=0,
∴b-a=0或c-a=0,解得b=a或c=a;
∵a,b,c 是△ABC的三条边长,
∴△ABC是等腰三角形;
故选B.
点评:本题主要考查了根的判别式、等腰三角形的判定.若关于其中一个未知数的一元二次方程有两个相等的实数根,则根的判别式△=0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
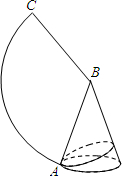 如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.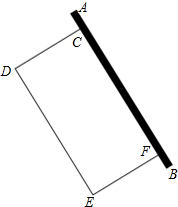 米1.75元,建新围栏的价格是每米4.5元,设利用旧围栏CF的长度为x米,修建草坪围栏所需的总费用为y元.
米1.75元,建新围栏的价格是每米4.5元,设利用旧围栏CF的长度为x米,修建草坪围栏所需的总费用为y元.