Question

如图是一个圆锥与其侧面展开图，已知圆锥的底面半径是2，母线长是6．
（1）求这个圆锥的高和其侧面展开图中∠ABC的度数；
（2）如果A是底面圆周上一点，从点A拉一根绳子绕圆锥侧面一圈再回到A点，求这根绳子的最短长度．

Answer 1

分析：（1）根据勾股定理直接求出圆锥的高，再利用圆锥侧面展开图弧长与其底面周长的长度关系，求出侧面展开图中∠ABC的度数即可；
（2）首先求出BD的长，再利用勾股定理求出AD以及AC的长即可．

解答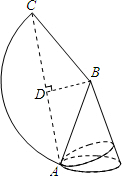：解：（1）圆锥的高=

62-22

=4

2

，
底面圆的周长等于：2π×2=

nπ×6

180

，
解得：n=120°；
                
（2）连结AC，过B作BD⊥AC于D，则∠ABD=60°．
由AB=6，可求得BD=3，
∴AD═3

3

，
AC=2AD=6

3

，
即这根绳子的最短长度是6

3

．

点评：此题考查了圆锥的计算；得到圆锥的底面圆的周长和扇形弧长相等是解决本题的突破点．