题目内容
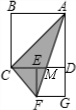 如图,点E在正方形ABCD的边CD上,四边形DEFG也是正方形,已知AB=a,DE=b(a、b为常数,且a>b>0),则△ACF的面积
如图,点E在正方形ABCD的边CD上,四边形DEFG也是正方形,已知AB=a,DE=b(a、b为常数,且a>b>0),则△ACF的面积
- A.只与a的大小有关
- B.只与b的大小有关
- C.只与CE的大小有关
- D.无法确定
A
分析:由题意,即可推出△ADM∽△FEM,依据相似三角形的性质可知,AD:EF=DM:EM,可得:DM:EM=a:b,由EM+DM=b,设EM=bx,EM=bx,即得x关于a、b表达式,便可推出EM关于a、b表达式,便可推出CM的长度,然后根据S△ACF=S△ACM+S△CMF= CM•AD+
CM•AD+ CM•EF=
CM•EF=
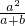 •(a+b),整理后,即可推出只与a的大小有关.
•(a+b),整理后,即可推出只与a的大小有关.
解答:∵正方形ABCD的边CD,四边形DEFG也是正方形,
∴AG∥EF,
∴△ADM∽△FEM,
∴AD:EF=DM:EM,
∵AB=a,DE=b,
∴DM:EM=a:b,
∵EM+DM=b,
设EM=bx,EM=bx,
∴ax+bx=b,
∴x=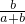 ,
,
∴EM= ,
,
∴CM=CE+EM=(a-b)+ =
= ,
,
∵S△ACF=S△ACM+S△CMF,
∴S△ACF= CM•AD+
CM•AD+ CM•EF
CM•EF
=
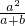 •(a+b)
•(a+b)
= ,
,
∴△ACF的面积只与a的大小有关系.
故选A.
点评:本题主要考查相似三角形的判定和性质、整式的混合运算、三角形的面积公式、正方形的性质,关键在于①正确认真的对相关整式进行整理,运算,②通过求证△ADM∽△FEM,推出EM的长度和CM的长度,根据图形明确△ACF的面积是△ACM和CMF的面积之和.
分析:由题意,即可推出△ADM∽△FEM,依据相似三角形的性质可知,AD:EF=DM:EM,可得:DM:EM=a:b,由EM+DM=b,设EM=bx,EM=bx,即得x关于a、b表达式,便可推出EM关于a、b表达式,便可推出CM的长度,然后根据S△ACF=S△ACM+S△CMF=
 CM•AD+
CM•AD+ CM•EF=
CM•EF=
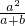 •(a+b),整理后,即可推出只与a的大小有关.
•(a+b),整理后,即可推出只与a的大小有关.解答:∵正方形ABCD的边CD,四边形DEFG也是正方形,
∴AG∥EF,
∴△ADM∽△FEM,
∴AD:EF=DM:EM,
∵AB=a,DE=b,
∴DM:EM=a:b,
∵EM+DM=b,
设EM=bx,EM=bx,
∴ax+bx=b,
∴x=
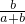 ,
,∴EM=
 ,
,∴CM=CE+EM=(a-b)+
 =
= ,
,∵S△ACF=S△ACM+S△CMF,
∴S△ACF=
 CM•AD+
CM•AD+ CM•EF
CM•EF=

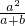 •(a+b)
•(a+b)=
 ,
,∴△ACF的面积只与a的大小有关系.
故选A.
点评:本题主要考查相似三角形的判定和性质、整式的混合运算、三角形的面积公式、正方形的性质,关键在于①正确认真的对相关整式进行整理,运算,②通过求证△ADM∽△FEM,推出EM的长度和CM的长度,根据图形明确△ACF的面积是△ACM和CMF的面积之和.

练习册系列答案
相关题目
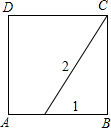 如图,点E在正方形ABCD的边AB上,若EB的长为1,EC的长为2,那么正方形ABCD的面积是( )
如图,点E在正方形ABCD的边AB上,若EB的长为1,EC的长为2,那么正方形ABCD的面积是( )A、
| ||
B、
| ||
| C、3 | ||
| D、5 |
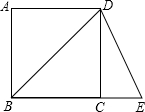 如图,点E在正方形ABCD的边BC的延长线上,如果BE=BD,那么∠E=
如图,点E在正方形ABCD的边BC的延长线上,如果BE=BD,那么∠E=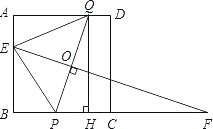 如图,点E在正方形ABCD的边AB上,AE=1,BE=2.点F在边BC的延长线上,且CF=BC;P是边BC上的动点(与点B不重合),PQ⊥EF,垂足为O,并交边AD于点Q;QH⊥BC,垂足为H.
如图,点E在正方形ABCD的边AB上,AE=1,BE=2.点F在边BC的延长线上,且CF=BC;P是边BC上的动点(与点B不重合),PQ⊥EF,垂足为O,并交边AD于点Q;QH⊥BC,垂足为H. (2013•资阳)如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
(2013•资阳)如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )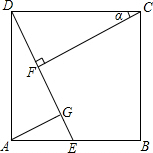 (2013•曲靖)如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.
(2013•曲靖)如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.