Question

【题目】边长为8的正方形ABCD中，点P在BC边上，CP=2，点Q为线段AP上一动点，射线BQ与正方形ABCD的一边交于点R，且AP=BR，那么____________

Answer 1

【答案】或1

【解析】

分两种情形：①当R在AD边上时，易得△AQR∽△PQB且相似比为1:1，从而得解；②当R在CD上时，先证明BR⊥AP，再根据等面积法计算BQ，根据线段的和差计算QR,计算比值即可得解.

①当R在AD边上时,

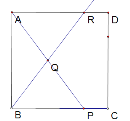
∵四边形ABCD为正方形

∴∠BAR=∠ABP=90°，AR∥BP

又∵AP=BR,AB=AB,

∴△ABP≌△BAR，

∴AR=BP，

∵AR∥BP,

∴△AQR∽△PQB

∴.

②当R在CD上时，

∵四边形ABCD为正方形

∴∠ABC=∠BCR=90°，AB=BC

又∵AP=BR

∴△ABP≌△BCR，

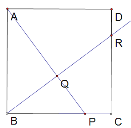
∴∠BAP=∠CBR，

∵∠CBR+∠ABR=90°，

∴∠BAP+∠ABR=90°，

∴∠AQB=90°，

∴BR⊥AP，

∵AB=8.BP=6，

∴AP=BR=，

∵ABBP=APBQ，

∴，

∴

故答案为1或.