题目内容
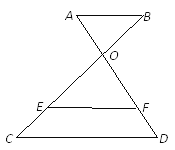
【题目】如图，已知AB∥EF∥CD，AD与BC相交于点O.
（1）如果CE=3，EB=9，DF=2，求AD的长；
（2）如果BO：OE：EC=2：4：3，AB=3，求CD的长．
【答案】（1）8；（2）
【解析】
试题（1）根据平行线分线段成比例、比例的基本性质求得AF=6，则AD=AF+FD=8；
（2）由BO：OE：EC=2：4：3，可得BO：CO=2：7，根据AB∥CD得△ABO∽△DCO，则可得出AB:CD=BO:CO，求出CD的值.
解：（1）∵AB∥EF∥CD，∴
=
，
又∵CE=3，EB=9，DF=2，∴
=
，得AF=6,
∴AD=AF+FD=8.
（2）∵BO：OE：EC=2：4：3，∴BO：CO=2：7，
∵AB∥CD，∴△ABO∽△DCO，
∴
=
=
，又AB=3，
∴CD=
.
练习册系列答案
相关题目
