题目内容
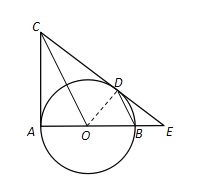
【题目】如图，
是
的直径，
是的切线，连结
，过点
作
交于点
，延长，
交于点
．
（1）求证：是的切线；
（2）若
，
，求的长．
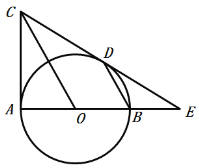
【答案】（1）见解析；（2）CD=12．
【解析】
（1）连接OD，根据切线的性质可得到∠OAC=90°，通过分析证明△CDO≌△CAO，可得OD⊥CE，即可得到结果；
（2）在Rt△ODE中，根据勾股定理可得圆的半径，根据平行线成比例得
，即可得到结果；
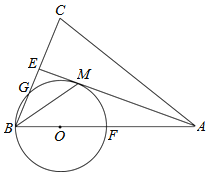
（1）证明：连接OD，
∵AC为⊙O的切线，
∴AC⊥AB．
∴∠OAC=90°．
∵BD∥OC，
∴∠OBD=∠AOC，∠ODB=∠COD．
∵OB、OD为⊙O的半径，
∴OB=OD．
∴∠OBD=∠ODB．
∴∠AOC=∠DOC．
在△CDO和△CAO中，
∴△CDO≌△CAO（SAS）
∴∠CDO=∠CAO=90°．
∴OD⊥CE于D，且OD是半径，
∴CE是⊙O的切线．
（2）解：在Rt△ODE中，∠ODE=90°，
∵
，
∴
，
∴
，
∵BD∥OC，
∴，
又BE=4，DE=8，BO=，
∴
，
∴
２．
【题目】合理饮食对学生的身体、智力发育和健康起到了极其重要的作用，只有荤食和素食的合理搭配，才能强化初中生的身体素质，某校为了解学生的体质健康状况，以便食堂为学生提供合理膳食，对本校七年级、八年级学生的体质健康状况进行了调查，过程如下：
收集数据：
从七、八年级两个年级中各抽取
名学生，进行了体质健康测试，测试成绩（百分制）如下：
七年级：
八年级：
整理数据：
年级 |
|
|
|
|
七年级 |
|
|
|
|
八年级 |
|
|
|
|
（说明：
为优秀，
为良好，
为及格，
为不及格）
分析数据：
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
（1）表格中
，
，
，
（2）比较这两组样本数据的平均数、中位数和众数，你认为哪个年级的体质健康成绩比较好？请说明理由
（3）若七年级共有
名学生，请估计七年级体质健康成绩优秀的学生人数
【题目】为增强学生垃圾分类意识，推动垃圾分类进校园．某初中学校组织全校1200名学生参加了“垃圾分类知识竞赛”，为了解学生的答题情况，学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析．
（1）学校设计了以下三种抽样调查方案：
方案一：从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析；
方案二：从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析；
方案三：从三个年级全体学生中随机抽取部分学生成绩进行调查分析．
其中抽取的样本具有代表性的方案是__________．（填“方案一”、“方案二”或“方案三”）
（2）学校根据样本数据，绘制成下表（90分及以上为“优秀”，60分及以上为“及格”）：
样本容量 | 平均分 | 及格率 | 优秀率 | 最高分 | 最低分 |
100 | 93.5 |
|
| 100 | 80 |
分数段统计（学生成绩记为 | |||||
分数段 |
|
|
|
|
|
频数 | 0 | 5 | 25 | 30 | 40 |
请结合表中信息解答下列问题：
①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内；
②估计该校1200名学生中达到“优秀”的学生总人数．
