题目内容
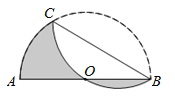
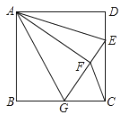
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,
,![]() 为
为![]() 边上一点(不与端点重合),将
边上一点(不与端点重合),将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
①![]() __________;
__________;
②若![]() 为
为![]() 的中点,则
的中点,则![]() 的面积为__________.
的面积为__________.
【答案】![]()
![]()
【解析】
①由折叠得∠DAE=∠FAE,AD=AF=AB,再由HL定理证明Rt△ABG≌Rt△AFG得∠BAG=∠FAG,从而可以求出∠EAG的度数;
②设BG=GF=y,则CG=a-y,由勾股定理得y的方程求得BG,GF,EF,再由同高的两个三角形的面积比等于底边之比,求得△CGF的面积.
解:①∵四边形ABCD是正方形,
∴AB=BC=AD=a,∠DAE=∠FAE.
∵将△ADE沿AE对折至△AFE,
∴∠AFE=∠ADE=∠ABG=90°,AF=AD=AB,EF=DE,∠DAE=∠FAE,
在Rt△ABG和Rt△AFG中,![]()
∴Rt△ABG≌Rt△AFG(HL),
∴∠BAG=∠FAG,
∴∠GAE=∠GAF+∠EAF=![]() ×90°=45°;
×90°=45°;
②若E为CD的中点,则DE=CE=EF=![]() a,
a,
设BG=GF=y,则CG=a-y,
CG2+CE2=EG2,
即(ay)2+(![]() a)2=(
a)2=(![]() a+y)2,
a+y)2,
解得y=![]() a,
a,
∴BG=GF=![]() a,CG=a-
a,CG=a-![]() a=
a=![]() a,
a,
∴![]() =
=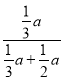 =
=![]() .
.
∴S△CFG=![]() S△CEG=
S△CEG=![]() ×
×![]() ×
×![]() a×
a×![]() a=
a=a2.
故答案为:①45°;②![]() a2.
a2.

【题目】生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的![]() 天数据,整理后绘制成统计表进行分析.
天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨) |
|
|
|
|
| 合计 |
频数 | 1 | 2 |
| 3 |
| |
频率 | 0.05 | 0.10 |
| 0.15 | 1 |
表中![]() 组的频率
组的频率![]() 满足
满足![]() .
.
下面有四个推断:
①表中![]() 的值为20;
的值为20;
②表中![]() 的值可以为7;
的值可以为7;
③这![]() 天的日均可回收物回收量的中位数在
天的日均可回收物回收量的中位数在![]() 组;
组;
④这![]() 天的日均可回收物回收量的平均数不低于3.
天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①②B.①③C.②③④D.①③④