题目内容
如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点P与点C不重合),连结BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连结AA1,射线AA1分别交射线PB、射线B1B于点E、F.
(1) 如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在 关系(填“相似”或“全等”),并说明理由;
(2)如图2,设∠ABP=β . 当60°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图3,当α=60°时,点E、F与点B重合. 已知AB=4,设DP=x,△A1BB1的面
积为S,求S关于x的函数关系式.
(1) 如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在 关系(填“相似”或“全等”),并说明理由;
(2)如图2,设∠ABP=β . 当60°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图3,当α=60°时,点E、F与点B重合. 已知AB=4,设DP=x,△A1BB1的面
积为S,求S关于x的函数关系式.

(1) 相似。理由见解析(2)存在,α=2β+60°(3)

解:(1) 相似 …………………………………………………………1分
由题意得:∠APA1=∠BPB1=α AP= A1P BP=B1P
则 ∠PAA1 =∠PBB1 = ……………………………2分
……………………………2分
∵∠PBB1 =∠EBF ∴∠PAE=∠EBF
又∵∠BEF=∠AEP
∴△BEF ∽△AEP………………………………………………………3分
(2)存在,理由如下: ………………………………………………………4分
易得:△BEF ∽△AEP
若要使得△BEF≌△AEP,只需要满足BE=AE即可 …………………5分
∴∠BAE=∠ABE
∵∠BAC=60° ∴∠BAE=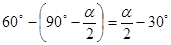
∵∠ABE=β ∠BAE=∠ABE ………………………………6分
∴ 即α=2β+60° ………………………………7分
即α=2β+60° ………………………………7分
(3)连结BD,交A1B1于点G,
过点A1作A1H⊥AC于点H.
∵∠B1 A1P=∠A1PA=60°∴A1B1∥AC
由题意得:AP= A1 P ∠A=60°
∴△PAA1是等边三角形
∴A1H= ………………………8分
………………………8分
在Rt△ABD中,BD=
∴BG= ……………………………… 9分
……………………………… 9分
∴ (0≤x<2)………………10分
(0≤x<2)………………10分
(1)通过三角形的相似性求证
(2)由(1)得△BEF ∽△AEP,若要使得△BEF≌△AEP,只需要满足BE=AE,即∠BAE=∠ABE,求得∠BAE的度数的表示,即可求出α与β之间的数量关系
(3)连结BD,交A1B1于点G,过点A1作A1H⊥AC于点H.由已知求得△PAA1是等边三角形,在Rt△ABD中,求得BG的长,从而通过三角形的面积,即可求得S关于x的函数关系式
由题意得:∠APA1=∠BPB1=α AP= A1P BP=B1P
则 ∠PAA1 =∠PBB1 =
 ……………………………2分
……………………………2分∵∠PBB1 =∠EBF ∴∠PAE=∠EBF
又∵∠BEF=∠AEP
∴△BEF ∽△AEP………………………………………………………3分
(2)存在,理由如下: ………………………………………………………4分
易得:△BEF ∽△AEP
若要使得△BEF≌△AEP,只需要满足BE=AE即可 …………………5分
∴∠BAE=∠ABE
∵∠BAC=60° ∴∠BAE=
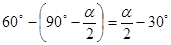
∵∠ABE=β ∠BAE=∠ABE ………………………………6分
∴
 即α=2β+60° ………………………………7分
即α=2β+60° ………………………………7分(3)连结BD,交A1B1于点G,
过点A1作A1H⊥AC于点H.
∵∠B1 A1P=∠A1PA=60°∴A1B1∥AC
由题意得:AP= A1 P ∠A=60°
∴△PAA1是等边三角形
∴A1H=
 ………………………8分
………………………8分在Rt△ABD中,BD=

∴BG=
 ……………………………… 9分
……………………………… 9分∴
 (0≤x<2)………………10分
(0≤x<2)………………10分(1)通过三角形的相似性求证
(2)由(1)得△BEF ∽△AEP,若要使得△BEF≌△AEP,只需要满足BE=AE,即∠BAE=∠ABE,求得∠BAE的度数的表示,即可求出α与β之间的数量关系
(3)连结BD,交A1B1于点G,过点A1作A1H⊥AC于点H.由已知求得△PAA1是等边三角形,在Rt△ABD中,求得BG的长,从而通过三角形的面积,即可求得S关于x的函数关系式

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目

 的图象过点(0,2),且
的图象过点(0,2),且  随
随 的增大而增大,则m=( )
的增大而增大,则m=( ) 为
为 ,运动时间为
,运动时间为 ,则下列图形能大致地刻画
,则下列图形能大致地刻画
 (年)逐年成直线上升,y与
(年)逐年成直线上升,y与

 、
、 两地相距10千米,甲班从
两地相距10千米,甲班从 小时,甲、乙两班离
小时,甲、乙两班离 千米、
千米、 千米,
千米,
 与时间
与时间 之间函数关系的是
之间函数关系的是