��Ŀ����
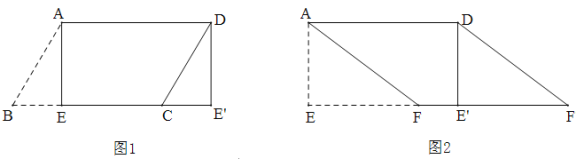
����Ŀ�� (1)��ͼ1��ֽƬ��ABCD�У�AD=5,S��ABCD=15,����A��AE��BC,����ΪE,��AE������ABE,����ƽ������DCE����λ�ã�ƴ���ı���AEE��D,���ı���AEE��D����״Ϊ�� ��
A.ƽ���ı��� B.���� C.���� D.������
(2)��ͼ2����(1)�е��ı���ֽƬAEE��D��,��EE����ȡһ��F,ʹEF=4��������AEF������ƽ������DE��F�� ��λ�ã�ƴ���ı���AFF��D
�� ��֤�ı���AFF��D������
�� ���ı���AFF��D�����Խ��ߵij�.
���𰸡���1��C����2����֤���μ��������� 3![]() ��
��![]() .
.
��������
�����������1�������������һ������ֱ�ǵ�ƽ���ı����Ǿ��μ��ɵó����ۣ���2���������AF�ij��ȣ������ڱ���ȵ�ƽ���ı��������μ��ɵó����ۣ�������AF��, DF,��Rt��AEF���У����ù��ɶ������AF'����Rt��DFE���������ù��ɶ������DF�����ǿ�֪�ı���AFF��D�����Խ��ߵij�.
���������(1)���������֪�ı���ABCD��ƽ���ı��Σ�AE��BC,��AEE'=90������Ϊ��һ������ֱ�ǵ�ƽ���ı����Ǿ��Σ���Cѡ����ȷ��(2) ����AF��DF����AF=DF��, ���ı���AFF��D��ƽ���ı��Σ���ΪS��ABCD=AD![]() AE=15, AD=5 ,����AE=3, ����ΪEF=4 ,��E=90��, ����AF=5, ��ΪAD=5 , ����AD=AF , ����ƽ���ı���AFF��D������. ����ͼ�� ����AF��, DF,
AE=15, AD=5 ,����AE=3, ����ΪEF=4 ,��E=90��, ����AF=5, ��ΪAD=5 , ����AD=AF , ����ƽ���ı���AFF��D������. ����ͼ�� ����AF��, DF,
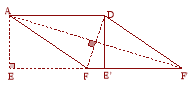
��Rt��AEF����AE=3, EF��=4+5=9, ����AF��=![]() =3
=3![]() ����Rt��DFE������FE��=5-4=1, DE��=AE=3, �ɹ��ɶ������DF=
����Rt��DFE������FE��=5-4=1, DE��=AE=3, �ɹ��ɶ������DF=![]() �������ı���AFF��D�����Խ��ߵij��ֱ���3
�������ı���AFF��D�����Խ��ߵij��ֱ���3![]() ��
��![]() .
.

 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�