题目内容
已知|a+2|与(b-3)2互为相反数,则ab=________.
-8
分析:根据非负数的性质解答.有限个非负数的和为零,那么每一个加数也必为零,即若a1,a2,…,an为非负数,且a1+a2+…+an=0,则必有a1=a2=…=an=0.
解答:∵|a+2|与(b-3)2互为相反数,
∴|a+2|+(b-3)2=0,
则a+2=0,a=-2;b-3=0,b=3.
故ab=(-2)3=-8.
点评:本题考查了非负数的性质,初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.
分析:根据非负数的性质解答.有限个非负数的和为零,那么每一个加数也必为零,即若a1,a2,…,an为非负数,且a1+a2+…+an=0,则必有a1=a2=…=an=0.
解答:∵|a+2|与(b-3)2互为相反数,
∴|a+2|+(b-3)2=0,
则a+2=0,a=-2;b-3=0,b=3.
故ab=(-2)3=-8.
点评:本题考查了非负数的性质,初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
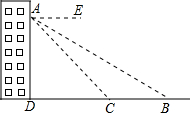 (2013•镇江)如图,小明在教学楼上的窗口A看地面上的B、C两个花坛,测得俯角∠EAB=30°,俯角∠EAC=45°.已知教学楼基点D与点C、B在同一条直线上,且B、C两花坛之间的距离为6m.求窗口A到地面的高度AD.(结果保留根号)
(2013•镇江)如图,小明在教学楼上的窗口A看地面上的B、C两个花坛,测得俯角∠EAB=30°,俯角∠EAC=45°.已知教学楼基点D与点C、B在同一条直线上,且B、C两花坛之间的距离为6m.求窗口A到地面的高度AD.(结果保留根号)