Question

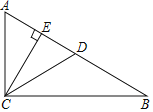
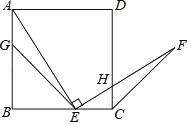
【题目】如图，G，E分别是正方形ABCD的边AB，BC上的点，且AG＝CE，AE⊥EF，AE＝EF，现有如下结论：①BE＝DH;②△AGE≌△ECF;③∠FCD＝45°;④△GBE∽△ECH．其中，正确的结论有（ ）

A. 4 个 B. 3 个 C. 2 个 D. 1 个

Answer 1

【答案】C

【解析】

由∠BEG＝45°知∠BEA＞45°，结合∠AEF＝90°得∠HEC＜45°，据此知 HC＜EC，即可判断①；求出∠GAE+∠AEG＝45°，推出∠GAE＝∠FEC，根据 SAS 推出△GAE≌△CEF，即可判断②；求出∠AGE＝∠ECF＝135°，即可判断③；求出∠FEC＜45°，根据相似三角形的判定得出△GBE和△ECH 不相似，即可判断④．

解：∵四边形 ABCD 是正方形，

∴AB＝BC＝CD，

∵AG＝GE，

∴BG＝BE，

∴∠BEG＝45°，

∴∠BEA＞45°，

∵∠AEF＝90°，

∴∠HEC＜45°，

∴HC＜EC，

∴CD﹣CH＞BC﹣CE，即 DH＞BE，故①错误；

∵BG＝BE，∠B＝90°，

∴∠BGE＝∠BEG＝45°，

∴∠AGE＝135°，

∴∠GAE+∠AEG＝45°，

∵AE⊥EF，

∴∠AEF＝90°，

∵∠BEG＝45°，

∴∠AEG+∠FEC＝45°，

∴∠GAE＝∠FEC，

在△GAE 和△CEF 中，

∵AG=CE，

∠GAE=∠CEF,

AE=EF,

∴△GAE≌△CEF（SAS））,

∴②正确；

∴∠AGE＝∠ECF＝135°，

∴∠FCD＝135°﹣90°＝45°，

∴③正确；

∵∠BGE＝∠BEG＝45°，∠AEG+∠FEC＝45°，

∴∠FEC＜45°，

∴△GBE 和△ECH 不相似，

∴④错误；

故选：C．