题目内容
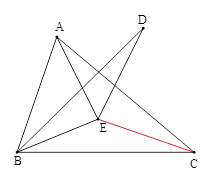
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连结AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
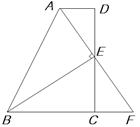
求证:(1)FC=AD;(2)AB=BC+AD.

求证:(1)FC=AD;(2)AB=BC+AD.
见解析
证明:(1)因为AD∥BC,E为CD的中点,
所以∠D=∠C,DE=EC.
又∠AED=∠FEC,所以△ADE≌△FCE.所以FC=AD.
(2)因为△ADE≌△FCE,所以AE=FE.
又因为BE⊥AE,所以BE是线段AF的垂直平分线,所以AB=FB.
因为FB=BC+FC=BC+AD,所以AB=BC+AD.
所以∠D=∠C,DE=EC.
又∠AED=∠FEC,所以△ADE≌△FCE.所以FC=AD.
(2)因为△ADE≌△FCE,所以AE=FE.
又因为BE⊥AE,所以BE是线段AF的垂直平分线,所以AB=FB.
因为FB=BC+FC=BC+AD,所以AB=BC+AD.

练习册系列答案
相关题目
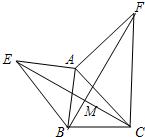
 ∠BAC,过点D作DE⊥AB,DE恰好是∠ADB的平分线,求证:CD=
∠BAC,过点D作DE⊥AB,DE恰好是∠ADB的平分线,求证:CD=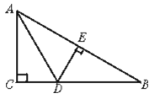
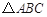 中,∠
中,∠ 90°,∠
90°,∠ 30°,以点
30°,以点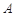 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交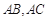 于点
于点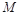 和
和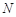 ,再分别以点
,再分别以点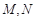 为圆心,大于
为圆心,大于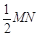 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点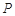 ,连接
,连接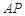 并延长交
并延长交 于点
于点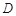 ,则下列说法中正确的个数 是( )
,则下列说法中正确的个数 是( )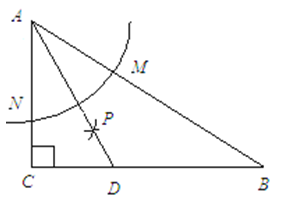
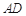 是∠
是∠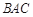 的平分线;②∠
的平分线;②∠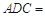 60°;③点
60°;③点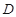 在
在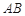 的中垂线上;④
的中垂线上;④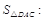
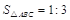 .
.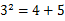
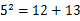
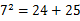
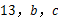
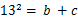
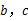 的值.
的值.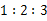 ,最短边长为1,最长边长为2.
,最短边长为1,最长边长为2.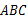 中,三边长满足
中,三边长满足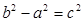 ,则互余的一对角是( )
,则互余的一对角是( )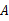 与∠
与∠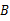
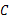 与∠
与∠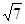 cm
cm