题目内容
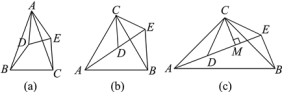
【题目】如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为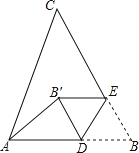
【答案】2 ![]()
【解析】解:如图,作DF⊥B′E于点F,作B′G⊥AD于点G,
∵∠B=60°,BE=BD=4,
∴△BDE是边长为4的等边三角形,
∵将△BDE沿DE所在直线折叠得到△B′DE,
∴△B′DE也是边长为4的等边三角形,
∴GD=B′F=2,
∵B′D=4,
∴B′G= ![]() =
= ![]() =2
=2 ![]() ,
,
∵AB=10,
∴AG=10﹣6=4,
∴AB′= ![]() =
= ![]() =2
=2 ![]() .故答案为:2
.故答案为:2 ![]() .
.
作DF⊥B′E于点F,作B′G⊥AD于点G,首先根据有一个角为60°的等腰三角形是等边三角形判定△BDE是边长为4的等边三角形,从而根据翻折的性质得到△B′DE也是边长为4的等边三角形,从而GD=B′F=2,然后根据勾股定理得到B′G=2 ![]() ,然后再次利用勾股定理求得答案即可.本题考查了翻折变换的性质,解题的关键是根据等边三角形的判定定理判定等边三角形,难度不大.
,然后再次利用勾股定理求得答案即可.本题考查了翻折变换的性质,解题的关键是根据等边三角形的判定定理判定等边三角形,难度不大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?