题目内容
【题目】(背景)如图(a),△ABC与△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
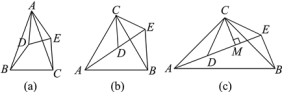
(探究)如图(b),△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为________;②线段BE与AD之间的数量关系是________.
(拓展)如图(c),△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①求∠AEB的度数;
②请直接写出线段CM,AE,BE之间的数量关系.
【答案】背景:见解析;探究:①60° ②BE=AD;拓展:(1)90°;(2)AE=BE+2CM
【解析】
背景:根据全等三角形的判定方法,判断出△BAD≌△CAE,即可判断出BD=CE;
探究:①根据△ACB和△DCE均为等边三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出∠BEC=∠ADC,进而判断出∠AEB的度数为60°即可;
②,由△ACD≌△BCE,即可判断出BE=AD;
拓展:①根据△ACB和△DCE均为等腰直角三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为90°即可;
②根据∠DCE=90°,CD=CE,CM⊥DE,可得CM=DM=EM,所以DE=DM+EM=2CM,据此判断出AE=BE+2CM即可.
背景:∵∠BAC=∠DAE=40°,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,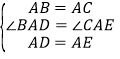 ,
,
∴△BAD≌△CAE,∴BD=CE;
探究:①∵△ACB和△DCE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,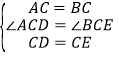 ,
,
∴△ACD≌△BCE,
∴∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180-60=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=120-60=60°,
故答案为:60°;
②∵△ACD≌△BCE,
∴BE=AD,
故答案为:BE=AD;
拓展:①∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,CD=CE,∠CDE=∠CED=45°,
∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
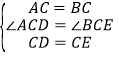 ,
,
∴△ACD≌△BCE,
∴AD=BE,∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180°-∠CDE=180°-45°=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°;
②∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM,
又∵AD=BE,
∴AE=AD+DE=BE+2CM

 阅读快车系列答案
阅读快车系列答案