题目内容
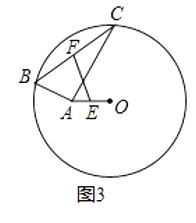
【题目】如图,在⊙O的内接五边形ABCDE中,∠B+∠E=215°,则∠CAD=°.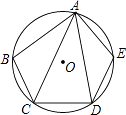
【答案】35
【解析】解:如图,连接CE,
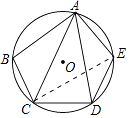
∵五边形ABCDE是圆内接五边形,
∴四边形ABCE是圆内接四边形,
∴∠B+∠AEC=180°,
∵∠B+∠AED=215°,
∴∠CED=35°,
∴∠CAD=∠CED=35°,
所以答案是:35.
【考点精析】认真审题,首先需要了解多边形内角与外角(多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°),还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键.

练习册系列答案
相关题目