题目内容
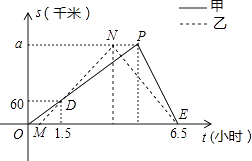
【题目】甲、乙两车从A地将一批物品匀速运往B地，甲出发0.5h后乙开始出发，结果比甲早1h到达B地．如图，线段OP、MN分别表示甲、乙两车离A地的距离S（km）与时间t（h）的关系，a表示A、B两地之间的距离．请结合图中的信息解决如下问题： 
（1）分别计算甲、乙两车的速度及a的值；
（2）乙车到达B地后以原速立即返回，请问甲车到达B地后以多大的速度立即匀速返回，才能与乙车同时回到A地？并在图中画出甲、乙两车在返回过程中离A地的距离S（km）与时间t（h）的函数图象．
【答案】
（1）解：甲的速度为60÷1.5=40（千米/小时），乙的速度为60千米/小时．
求a的方法如下：
方法1：由题意， 
= 
﹣1﹣0.5，
解得：a=180；
方法2：设甲到达B地的时间为t，则乙所用时间为：t﹣1﹣0.5，由路程相等得，
40t=60（t﹣1﹣0.5），
解得：t=4.5，
a=40t=40×4.5=180；
方法3：由题意知，M（0.5，0），
可求得线段OP、MN表示的函数关系式分别为：S甲=40t，S乙=60t﹣30，
设N（t，a），P（t+1，a），代入函数关系式，
，
解得： 
（2）解：方法1：设甲返回的速度为xkm/h，则：
﹣1= 
，
解得：x=90，
经检验得出：x=90是方程的根且符合题意，
故甲返回的速度为90km/h，
方法2：设甲返回的速度为xkm/h，则 ×2+0.5= 
+ ，
解得：x=90，
经检验得出：x=90是方程的根且符合题意，
故甲返回的速度为90km/h，
方法3，：如图，线段PE、NE分别表示甲、乙两车返回时距离A地的距离S（千米）与时间t（小时）的关系，
点E的横坐标为： ×2+0.5=6.5，若甲、乙两车同时返回A地，则甲返回时需用时间为：
6.5﹣ =2（小时），
故甲返回的速度为90km/h，如图所示．
【解析】（1）利用图象上D点的坐标得出甲的速度为40千米/小时，乙的速度为60千米/小时，再利用两车行驶时间列出等量关系求出a即可；（2）首先设甲返回的速度为xkm/h，则利用返回时两人所用时间相差1小时得出 ﹣1= ，进而求出即可．
【题目】在大课间活动中，体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试，并对成绩进行统计分析，绘制了频数分布表和统计图，请你根据图表中的信息完成下列问题：
分 组 | 频数 | 频率 |
第一组（0≤x＜15） | 3 | 0.15 |
第二组（15≤x＜30） | 6 | a |
第三组（30≤x＜45） | 7 | 0.35 |
第四组（45≤x＜60） | b | 0.20 |
（1）频数分布表中a= ， b= ， 并将统计图补充完整；
（2）如果该校七年级共有女生180人，估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人？
（3）已知第一组中只有一个甲班学生，第四组中只有一个乙班学生，老师随机从这两个组中各选一名学生谈心得体会，则所选两人正好都是甲班学生的概率是多少？
【题目】如图，某中学为合理安排体育活动，在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1000名学生中，随机抽取了若干名学生进行调查，了解学生最喜欢的一种球类运动，每人只能在这五种球类运动中选择一种．调查结果统计如下：
球类名称 | 乒乓球 | 排球 | 羽毛球 | 足球 | 篮球 |
人数 | a | 12 | 36 | 18 | b |
解答下列问题：
（1）本次调查中的样本容量是；
（2）a= ， b=；
（3）试估计上述1000名学生中最喜欢羽毛球运动的人数．
