题目内容
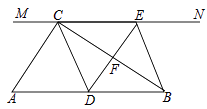
【题目】如图1,在数轴上A点表示数a,B点表示数b,a、b满足|a+2|+|b-6|=0。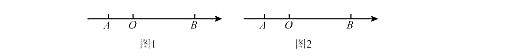
(1)点A表示的数为,点B表示的数为;
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=BC,则C点表示的数为;
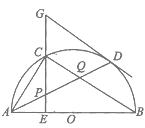
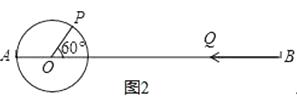
(3)如图2,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左动。在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒)。
①分别表示出甲、乙两小球到原点的距离(用t表示)
②求甲、乙两小球到原点的距离相等时经历的时间。
【答案】
(1)-2
,6
(2)2
(3)①t+2;②6-2t或2t-6;
【解析】(1)∵|a+2|+|b-6|=0,
∴a+2=0,b-6=0,
解得,a=-2,b=6,
∴点A表示的数为-2,点B表示的数为 6.
故填:-2、6;
(2)设数轴上点C表示的数为c.
∵AC=BC,
∴|c-a|=|c-b|,即|c+2|=|c-6|.
c=2
(3)①∵甲球运动的路程为:1![]() t=t,OA=2,
t=t,OA=2,
∴甲球与原点的距离为:t+2;
乙球到原点的距离分两种情况:
(Ⅰ)当0<t≤3时,乙球从点B处开始向左运动,一直到原点O,
∵OB=6,乙球运动的路程为:2t=2t,
乙到原点的距离:6-2t(0≤t≤3)
(Ⅱ)当t>3时,乙球从原点O处开始一直向右运动,
此时乙球到原点的距离为:2t-6 (t>3);
②当0<t≤3时,得t+2=6-2t,
解得t=![]() ;
;
当t>3时,得t+2=2t-6,
解得t=8.
故当t=![]() 秒或t=8秒时,甲乙两小球到原点的距离相等
秒或t=8秒时,甲乙两小球到原点的距离相等
(1)利用绝对值的非负性,可得出每个数为0,可求出结果;(2)利用绝对值的几何意义,中点公式,可求出c;(3)数轴上点之间的距离可表示为AB=XA-XB (A右,B左),需分类讨论,分哪个点在右侧或左侧讨论.

【题目】体育课上全班男生进行了百米测试,达标成绩为14秒,下面是第一小组8名男生的成绩记录,其中“+”表示成绩大于14秒,“﹣”表示成绩小于14秒
﹣1 | +0.8 | 0 | ﹣1.2 | ﹣0.1 | 0 | +0.5 | ﹣0.6 |
(1)求这个小组的男生达标率是多少?
(2)求这个小组8名男生的平均成绩是多少?
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
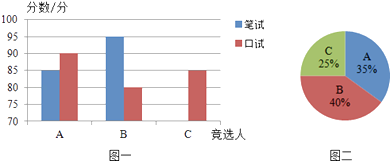
(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.